The H.C.F of two equal positive integers k, k is : Solution in Tamil
The correct Answer is:k
Step by step video, text & image solution for The H.C.F of two equal positive integers k, k is : by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NUMBERS AND SEQUENCESBOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - ACTIVITIES
9 Videos
- NUMBERS AND SEQUENCESBOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
23 Videos
- NUMBERS AND SEQUENCESBOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - THINKING CORNER
13 Videos
- MENSURATIONBOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
16 Videos
- RELATIONS AND FUNCTION BOOK - PREMIERS PUBLISHERSCHAPTER - RELATIONS AND FUNCTION EXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
25 Videos
Similar Questions
This activity helps you to find H.C.F. of two positive numbers. We first observe the following instructions.
Construct a rectangle whose length and breadth are the given numbers.
View SolutionThe quotient and remainder when 19 is divided by −3 are :
View SolutionWhen a positive integer is divided by 3
What are the possible remainders?
View SolutionMatch the following:
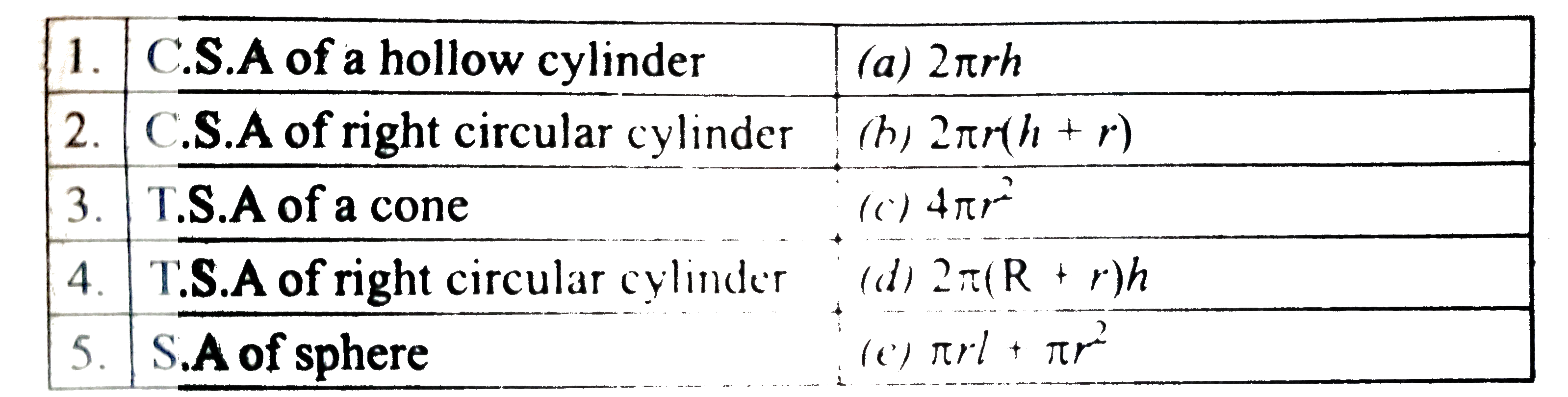
View SolutionIf n(A×B)=24andA={1,3,5,7}then n (B) is
View Solutionsum_(k=1)^(360)(1)/(k sqrt(k+1)+(k+1)sqrt(k)) is the ratio of two relatively prime positive integers m and n then the value of m+n is equal to
View SolutionFor which positive integers n is the ratio (sum_(k=1)^(n)k^(2))/(sum_(k=1)^(n)k) an integer?
View SolutionIf N is the largest possible value of K for which 3^(11) can be expressed as a sum of k consecutive positive integers,then sum of digit of K is equal to.
View SolutionFor a real number r let [r] denote the largest integer less than or equal to r. Let a>1 be a real number which is not an integer and let k be the smallest positive integer positive integer such that [ak]>[a]k. Then which of the following statements is always true?
View SolutionFor which positive integers n is the ratio, ∑+(k=1)nk2∑nk=1k an integer ?
View SolutionIf n is a positive integer and Ck=nCk, then the value of n∑k=1k3(CkCk−1)2 equals:
View SolutionIf a and b are two positive integers, then the relation between their L.C.M and H.C.F will be :
View SolutionThe relation between L.C.M. and H.C.F. of two positive integers will be
View SolutionFor any odd prime number p there exists a positive integer k where 1<k<p, such that the remainder of k2p is 1. Then the number of positive integers k is :
View SolutionThe positive integer k for which ((101)^(k/2))/k! is maximum is
View Solution
