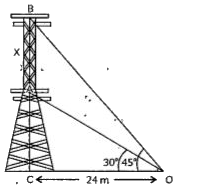
The height AC is:
13.84 m
14.6 m
16.7 m
34.6 m
The correct Answer is:A
Step by step video & image solution for The height AC is: by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 4BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - PART-B(SECTION-III)
9 Videos
- SAMPLE PAPER 4BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - PART-B(SECTION-IV)
10 Videos
- SAMPLE PAPER 4BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - PART-A(SECTION-I)
21 Videos
- SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]EXERCISE - SECTION - D
12 Videos
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - PART - B (SECTION - V)
4 Videos
Similar Questions
ΔABC is isosceles with AB=AC=7.5cmandBC=13cmandAC=12cm. The height AD from A to BC is 6cm. Find the area of ΔABC. What will be the height from C to AB,CE
View SolutionTriangle ABC is isosceles with AB=AC=7.5 cm and BC=9 cm . The height from A to BC i.e, AD is 6 cm. Find the area of ABC. what will be the height from C to AB?
View Solution
Knowledge Check
The length of AC isA22.8 mB26 mC25.6 mD33 mABC is an isosceles triangle with AB = AC. Side BA is produced to D such that AB=AD. Find the ∠BCD:
A100∘B60∘C80∘D90∘The average of height of 16 students is 142 cm. If the height of the teacher is included, the average height increases by 1 cm. The height of the teacher is
A156 cmB159 cmC158 cmD157 cm
EXAMPLE 12 Triangle ABC is isosceles with AB=AC=7.5cmandBC=9cm. The height from A to BC i.e. AD is 6 cm. Find the area of ΔABC. What will be the height from C to AB ?
View SolutionThe height of Apala is 150 cm. The height of Pari is 120 cm. The ratio of theh height of Apala to the height of Pari is
View Solutionvolume of a rectangular box (cuboid) with length=2ab, breadth=3ac and height=2ac is
View SolutionABC is a triangular park with AB = AC = 100 m. A block tower is situated at the midpoint of BC.The angles of elevation of the top of the tower at A and B are cot−1(3.2) and cosec−1(2.6) respectively.The height of the tower is:
View SolutionABC is a triangular park with AB = AC = 100 m. A block tower is situated at the midpoint of BC.The angles of elevation of the top of the tower at A and B are cot−1(3.2) and cosec−1(2.6) respectively.The height of the tower is:
View Solution
