The height of a cone is 21cm. Find the area of the base if the slant height is 28cm.
To solve the problem step by step, we will follow the mathematical concepts and formulas related to the geometry of a cone.
Step 1: Write down the given information
- Height of the cone (H) = 21 cm
- Slant height of the cone (L) = 28 cm
Step 2: Use the Pythagorean theorem to find the radius (r)
The relationship between the height (H), radius (r), and slant height (L) of a cone can be expressed using the Pythagorean theorem:
L2=H2+r2
Substituting the known values:
282=212+r2
Step 3: Calculate 282 and 212
- 282=784
- 212=441
Now substitute these values into the equation:
784=441+r2
Step 4: Solve for r2
To find r2, rearrange the equation:
r2=784−441
r2=343
Step 5: Find the area of the base of the cone
The area of the base (A) of a cone is given by the formula:
A=πr2
Substituting the value of r2:
A=π×343
Using the approximate value of π=227:
A=227×343
Step 6: Calculate the area
To simplify:
1. Divide 343 by 7:
343÷7=49
2. Now multiply by 22:
A=22×49=1078
Final Answer
The area of the base of the cone is:
A=1078cm2
---
- Height of the cone (H) = 21 cm
- Slant height of the cone (L) = 28 cm
The relationship between the height (H), radius (r), and slant height (L) of a cone can be expressed using the Pythagorean theorem:
L2=H2+r2
282=212+r2
- 282=784
- 212=441
784=441+r2
To find r2, rearrange the equation:
r2=784−441
r2=343
The area of the base (A) of a cone is given by the formula:
A=πr2
A=π×343
A=227×343
To simplify:
1. Divide 343 by 7:
343÷7=49
A=22×49=1078
The area of the base of the cone is:
A=1078cm2
Topper's Solved these Questions
- BOOK - RD SHARMA ENGLISHCHAPTER - SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDEREXERCISE - All Questions133videos
SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDER
- BOOK - RD SHARMA ENGLISHCHAPTER - SURFACE AREA AND VOLUME OF A SPHERE EXERCISE - All Questions140videos
SURFACE AREA AND VOLUME OF A SPHERE
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the area of a triangle with base = 18 cm and height = 12 cm.
A128 sq. cmB110 sq. cmC108 sq. cmD109 sq. cm
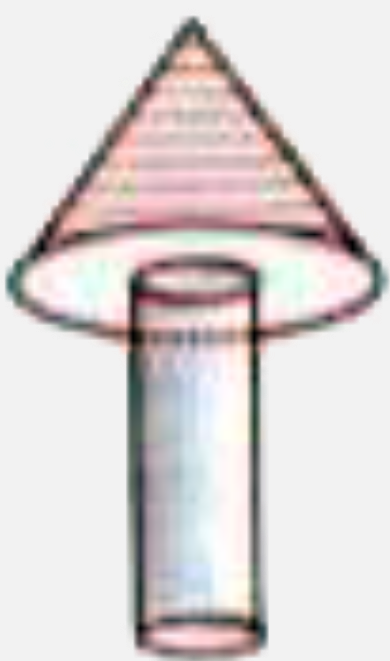
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside If the height of the cone is 24 cm the total height of the toy is 60 cm and the radius of the base of the cone= twice the radius of the base of the cylinder = 10 cm .Find the total surface area of the you.
 View Solution
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside.
If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm, find the total surface area of the toy. Take π=3.14]
 View Solution
View SolutionThe surface area of a solid metallic sphere is 616 cm2 . It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed (Use π=22/7 )
View SolutionThe height of a right circular cone is 7 cm and radius is 24 cm. Find the slant height of the cone.
View SolutionFind the volume of a cone having radius of the base 35 cm and slant height 37 cm.
View SolutionThe volume of a right circular cone is 9856cm3. If the diameter of the base is 28 cm. Find (i) height of the cone (ii) slant height of the cone (iii) curved surface area of the cone
View SolutionThe slant height of a cone is 10.5 cm and diametre of base is 14 cm. Find its curved surface area.
View Solution

