The index number of the following data for the year 2019, taking 2018 as base year was found to be 116. The simple aggregate method was used for calculation. Find numerical value of a, b, if the sum of prices is, the year 2019 is ₹ 203.
The correct Answer is:30.43
To solve the problem, we need to find the values of a and b given the index number for the year 2019 and the prices for the year 2018. We will use the simple aggregate method for index number calculation.
1. Understanding the Given Information:
- The index number for 2019 (taking 2018 as the base year) is given as 116.
- The sum of prices for the year 2019 is ₹ 203.
- The prices for the year 2018 are provided for items A, B, C, D, E, and F.
2. Using the Formula for Simple Aggregate Index:
The formula for the simple aggregate index number is:
P01=∑P1∑P0×100
Where:
- P01 is the index number (116 in this case).
- ∑P1 is the sum of prices in the current year (2019), which is ₹ 203.
- ∑P0 is the sum of prices in the base year (2018).
3. Setting Up the Equation:
From the formula, we can rearrange it to find ∑P0:
116=203∑P0×100
Rearranging gives:
∑P0=203×100116
4. Calculating ∑P0:
∑P0=20300116≈175
5. Finding the Value of a:
The sum of prices in the base year (2018) is:
10+20+25+30+a+50=135+a
Setting this equal to ∑P0:
135+a=175
Solving for a:
a=175−135=40
6. Finding the Value of b:
The sum of prices in the current year (2019) is:
30+25+45+15+35+b=150+b
Setting this equal to ∑P1:
150+b=203
Solving for b:
b=203−150=53
Final Values:
- a=40
- b=53
- The index number for 2019 (taking 2018 as the base year) is given as 116.
- The sum of prices for the year 2019 is ₹ 203.
- The prices for the year 2018 are provided for items A, B, C, D, E, and F.
The formula for the simple aggregate index number is:
P01=∑P1∑P0×100
Where:
- P01 is the index number (116 in this case).
- ∑P1 is the sum of prices in the current year (2019), which is ₹ 203.
- ∑P0 is the sum of prices in the base year (2018).
From the formula, we can rearrange it to find ∑P0:
116=203∑P0×100
Rearranging gives:
∑P0=203×100116
∑P0=20300116≈175
The sum of prices in the base year (2018) is:
10+20+25+30+a+50=135+a
Setting this equal to ∑P0:
135+a=175
Solving for a:
a=175−135=40
The sum of prices in the current year (2019) is:
30+25+45+15+35+b=150+b
Setting this equal to ∑P1:
150+b=203
Solving for b:
b=203−150=53
- a=40
- b=53
Topper's Solved these Questions
Similar Questions
The index number for the following data for the year 2008, taking 200 4 as base year was found to be 116. The simple aggregate method was used for calculation. Find the numerical value of xandy if the sum of the prices in the year 2008 is Rs. 203.
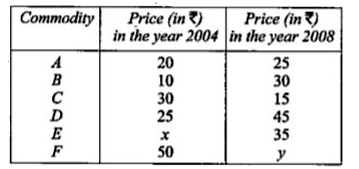
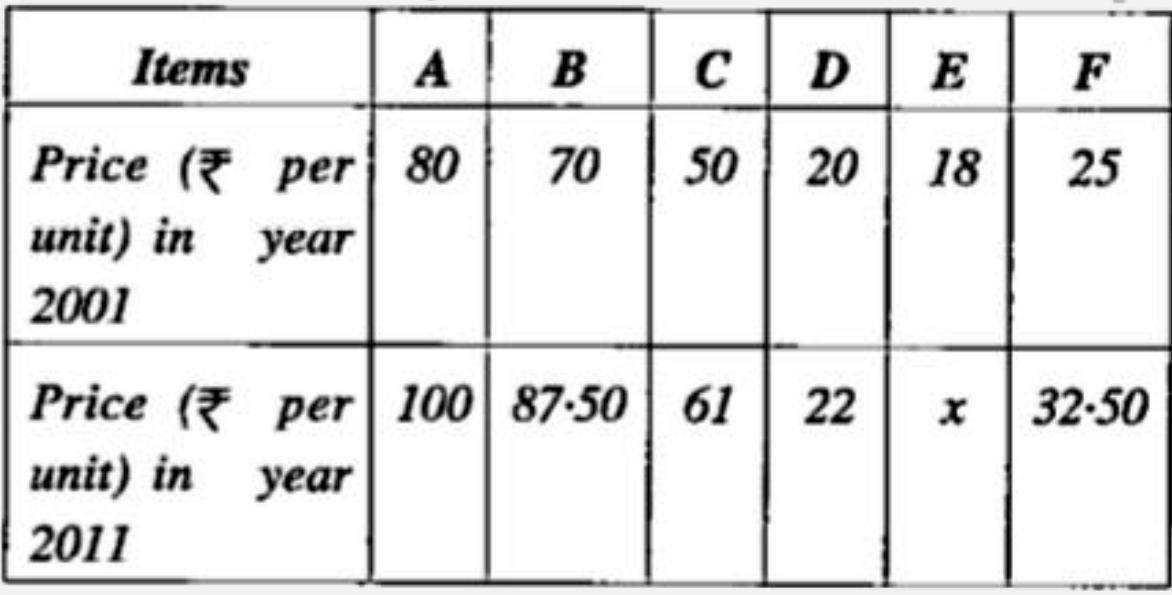
View SolutionThe price index for the following data for the year 2011 taking 2001 as the base year was 127. The simple average of price relatives method was used. Find the value of x :
View Solution
Knowledge Check
Index number calculated for the year 2019 using 2015 as the base year is 114.9 .If commodity is sold for Rs 5.75 in 2015 , then the selling price in 2019 is
ARs 7.57BRs 6.61CRs6.16DRs 66.1
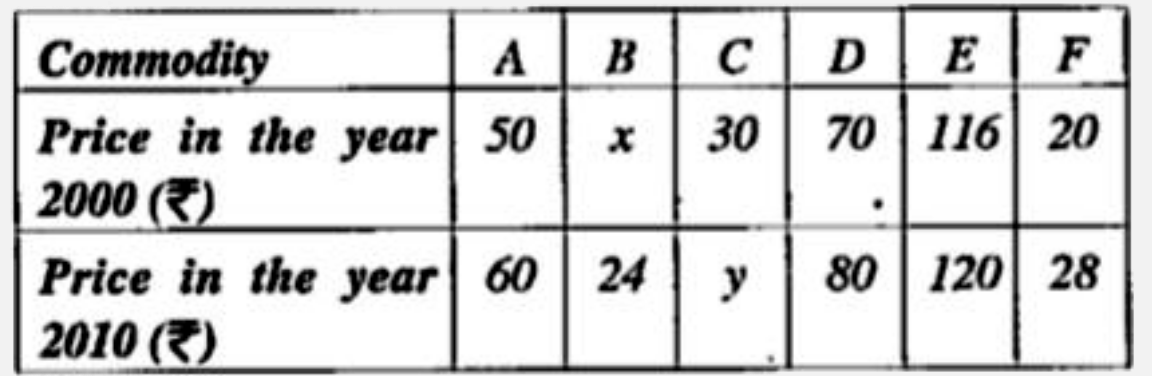
The index number by the method of aggregates for the year 2010, taking 2000 as the base year, was found to be 116. If sum of the prices in the year 2000 is Rs. 300, find the values of x and y in the data given below:
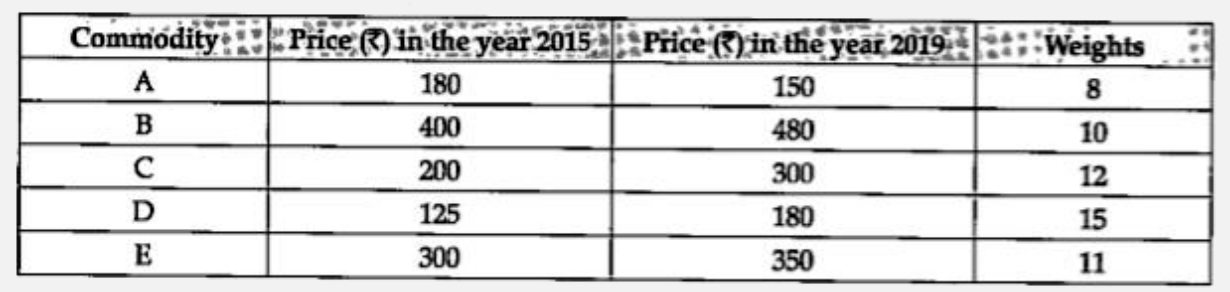
View SolutionCalculate the index number for year 2019 with 2015 as base year by weighted aggregate method.
View SolutionThe index number for the year 2005 taking 2000 as base year for the following data was found to be 125. Find the missing entries in the data if ∑p0=360.

View SolutionConstruct the index numbers for 2014 taking 2010 as the base year from the following data by simple average of price relative method:

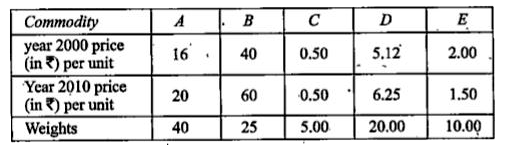
View SolutionFind the consumer price index number for the year 2010 as the base year 2000 by using method of weighted aggregates.
View SolutionConstruct the index number for 1991 taking 1990 as the base year from the following data by simple average of price relative method.

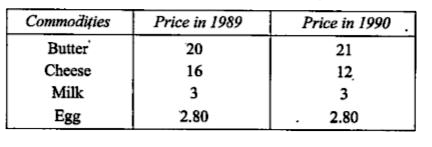
View SolutionConstruct the consumer price index number for 1990, taking 1989 as the base year and using simple average of price relative method for the following data:
View Solution
