The length of the tangent of the ellipse x225+y216=1 intercepted between auxiliary circle such that the portionof the tangent intercepted between the auxiliary circle subtends equal angles at foci is
6
3
4
8
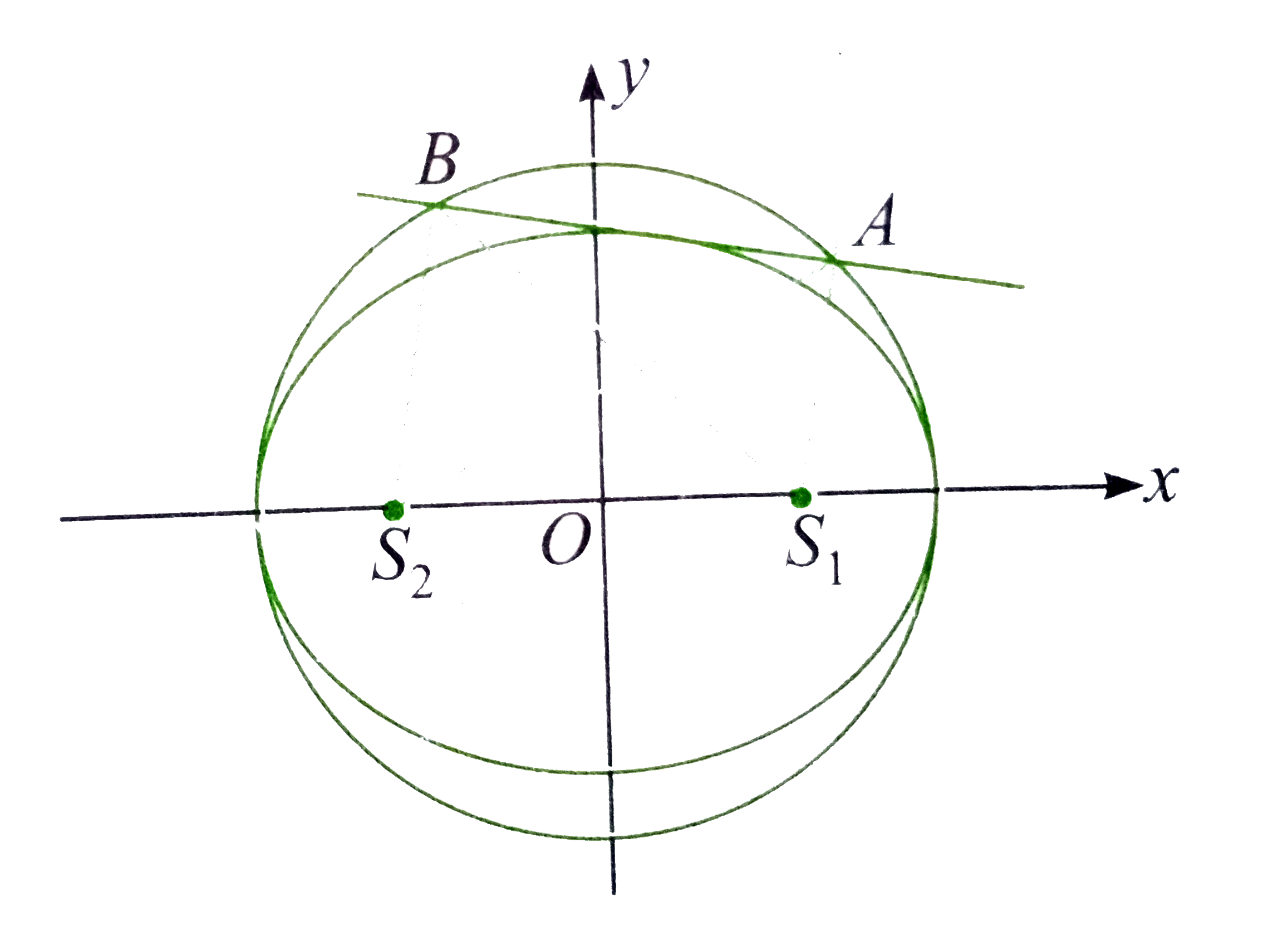
Let AB be the length of the tangent intercepted by auxiliary circle and S1,S2 be the foci.
Given that
∠AS1B=∠AS2B
⇒∠S1AB=∠S2AB=π2
So AS1S2B is a rectangle.
∴AB=S1S2=2aex=2×5×35=6
Similar Questions
The equations of the tangents to the ellipse 3x2+y2=3 making equal intercepts on the axes are
View SolutionIf any tangent to the ellipse x2a2+y2b2=1 intercepts equal lengths l on the axes, then find l.
View SolutionStatement 1: In the parabola y2=4ax, the circle drawn the taking the focal radii as diameter touches the y-axis. Statement 2: The portion of the tangent intercepted between the point of contact and directrix subtends an angle of 900 at focus.
View SolutionThe equation of the tangents to the circle x2+y2=25 with slope 2 is
View SolutionProve that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre.
View SolutionIf the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View SolutionProve that the portion of the tangent to an ellipse intercepted between the ellipse and the directrix subtends a right angle at the corresponding focus.
View SolutionFind all the curves y=f(x) such that the length of tangent intercepted between the point of contact and the x-axis is unity.
View SolutionThe exhaustive set of values of α2 such that there exists a tangent to the ellipse x2+α2y2=α2 and the portion of the tangent intercepted by the hyperbola α2x2−y2=1 subtends a right angle at the center of the curves is:
View SolutionShow that the length of the tangent to the parabola y2=4ax intercepted between its point of contact and the axis of the parabola is bisected by the tangent at the vertex.
View Solution

