The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and the data obtained is represented in the following table: Length (mm): 118-126 127-135 136-144 145-153 154-162 163-171 172-180 No. of leaves: 3 5 9 12 5 4 2. Find the mean length of leaf.
To find the mean length of the leaves based on the given data, we will follow these steps:
Step 1: Create a Frequency Table
We start by creating a frequency table that includes the class intervals, their mid-values (class marks), and the frequencies.
| Length (mm) | Frequency (f) |
|--------------|---------------|
| 118 - 126 | 3 |
| 127 - 135 | 5 |
| 136 - 144 | 9 |
| 145 - 153 | 12 |
| 154 - 162 | 5 |
| 163 - 171 | 4 |
| 172 - 180 | 2 |
Step 2: Convert to Inclusive Class Intervals
Since the lengths are measured to the nearest millimeter, we convert the intervals to inclusive class intervals:
| Length (mm) | Frequency (f) |
|----------------|---------------|
| 117.5 - 126.5 | 3 |
| 126.5 - 135.5 | 5 |
| 135.5 - 144.5 | 9 |
| 144.5 - 153.5 | 12 |
| 153.5 - 162.5 | 5 |
| 162.5 - 171.5 | 4 |
| 171.5 - 180.5 | 2 |
Step 3: Calculate the Mid-Values (Class Marks)
Next, we calculate the mid-value (x_i) for each class interval:
- For 117.5 - 126.5: (117.5 + 126.5) / 2 = 122
- For 126.5 - 135.5: (126.5 + 135.5) / 2 = 131
- For 135.5 - 144.5: (135.5 + 144.5) / 2 = 140
- For 144.5 - 153.5: (144.5 + 153.5) / 2 = 149
- For 153.5 - 162.5: (153.5 + 162.5) / 2 = 158
- For 162.5 - 171.5: (162.5 + 171.5) / 2 = 167
- For 171.5 - 180.5: (171.5 + 180.5) / 2 = 176
Step 4: Create a New Table with Mid-Values
Now we create a new table that includes the mid-values and their corresponding frequencies.
| Length (mm) | Mid-Value (x_i) | Frequency (f) | f * x_i |
|----------------|------------------|---------------|---------|
| 117.5 - 126.5 | 122 | 3 | 366 |
| 126.5 - 135.5 | 131 | 5 | 655 |
| 135.5 - 144.5 | 140 | 9 | 1260 |
| 144.5 - 153.5 | 149 | 12 | 1788 |
| 153.5 - 162.5 | 158 | 5 | 790 |
| 162.5 - 171.5 | 167 | 4 | 668 |
| 171.5 - 180.5 | 176 | 2 | 352 |
| Total | | 40 | 5879|
Step 5: Calculate the Mean
To find the mean length of the leaves, we use the formula:
Mean(¯x)=∑(fi⋅xi)∑fi
Substituting the values we calculated:
¯x=587940=146.975
Final Answer
The mean length of the leaves is approximately 146.98 mm.
---
We start by creating a frequency table that includes the class intervals, their mid-values (class marks), and the frequencies.
|--------------|---------------|
| 118 - 126 | 3 |
| 127 - 135 | 5 |
| 136 - 144 | 9 |
| 145 - 153 | 12 |
| 154 - 162 | 5 |
| 163 - 171 | 4 |
| 172 - 180 | 2 |
Since the lengths are measured to the nearest millimeter, we convert the intervals to inclusive class intervals:
|----------------|---------------|
| 117.5 - 126.5 | 3 |
| 126.5 - 135.5 | 5 |
| 135.5 - 144.5 | 9 |
| 144.5 - 153.5 | 12 |
| 153.5 - 162.5 | 5 |
| 162.5 - 171.5 | 4 |
| 171.5 - 180.5 | 2 |
Next, we calculate the mid-value (x_i) for each class interval:
- For 126.5 - 135.5: (126.5 + 135.5) / 2 = 131
- For 135.5 - 144.5: (135.5 + 144.5) / 2 = 140
- For 144.5 - 153.5: (144.5 + 153.5) / 2 = 149
- For 153.5 - 162.5: (153.5 + 162.5) / 2 = 158
- For 162.5 - 171.5: (162.5 + 171.5) / 2 = 167
- For 171.5 - 180.5: (171.5 + 180.5) / 2 = 176
Now we create a new table that includes the mid-values and their corresponding frequencies.
|----------------|------------------|---------------|---------|
| 117.5 - 126.5 | 122 | 3 | 366 |
| 126.5 - 135.5 | 131 | 5 | 655 |
| 135.5 - 144.5 | 140 | 9 | 1260 |
| 144.5 - 153.5 | 149 | 12 | 1788 |
| 153.5 - 162.5 | 158 | 5 | 790 |
| 162.5 - 171.5 | 167 | 4 | 668 |
| 171.5 - 180.5 | 176 | 2 | 352 |
| Total | | 40 | 5879|
To find the mean length of the leaves, we use the formula:
The mean length of the leaves is approximately 146.98 mm.
Topper's Solved these Questions
Similar Questions
The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table: (i) Draw a histogram to represent the given data.(ii) Is there any other suitable graphical representation for the same data?(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long?Why?
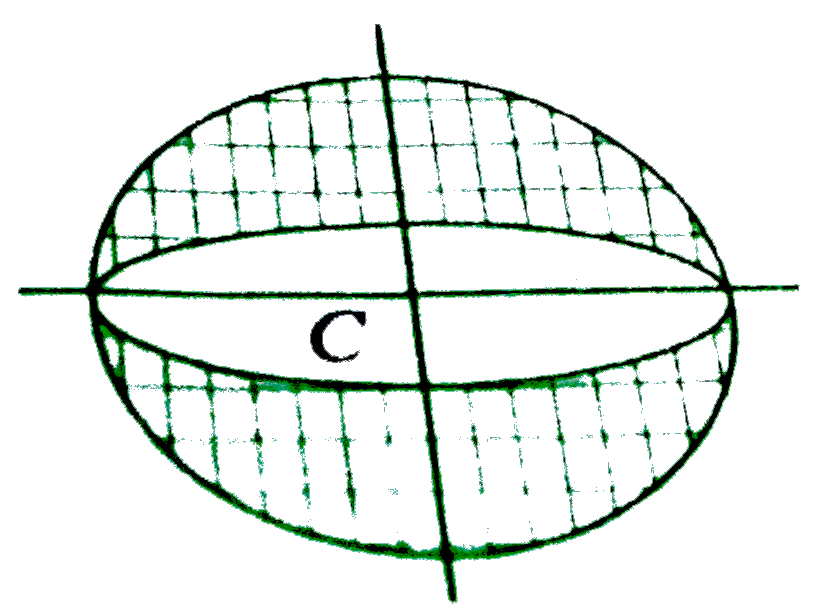
View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet isView SolutionConstruct a frequency distribution table for the following data, taking class-intervals 4−6,6−8, ............., 14−16.
11.5,6.3,7.8,9.2,10.5,
4.5,6,8.3,12.5,15.8,
7.4,5.3,8.4,15.2,8.9,
9.8,8.25,6.5,5.8,10.5,
14.2,15.3,11.7,9.9,8.8,
6.6,4.3,4.7,9.4,10.1,
15.5,14.4,12.2,7.7,5.5.View Solution

