The line passing through the extremity A of the major axis and extremity B of the minor axis of the ellipse x2+9y2=9 meets is auxiliary circle at the point M. Then the area of the triangle with vertices at A,M, and O (the origin) is (a) 31/10 (b) 29/10 (c) 21/10 (d) 27/10Solution in Bengali
31/10
29/10
21/10
27/10
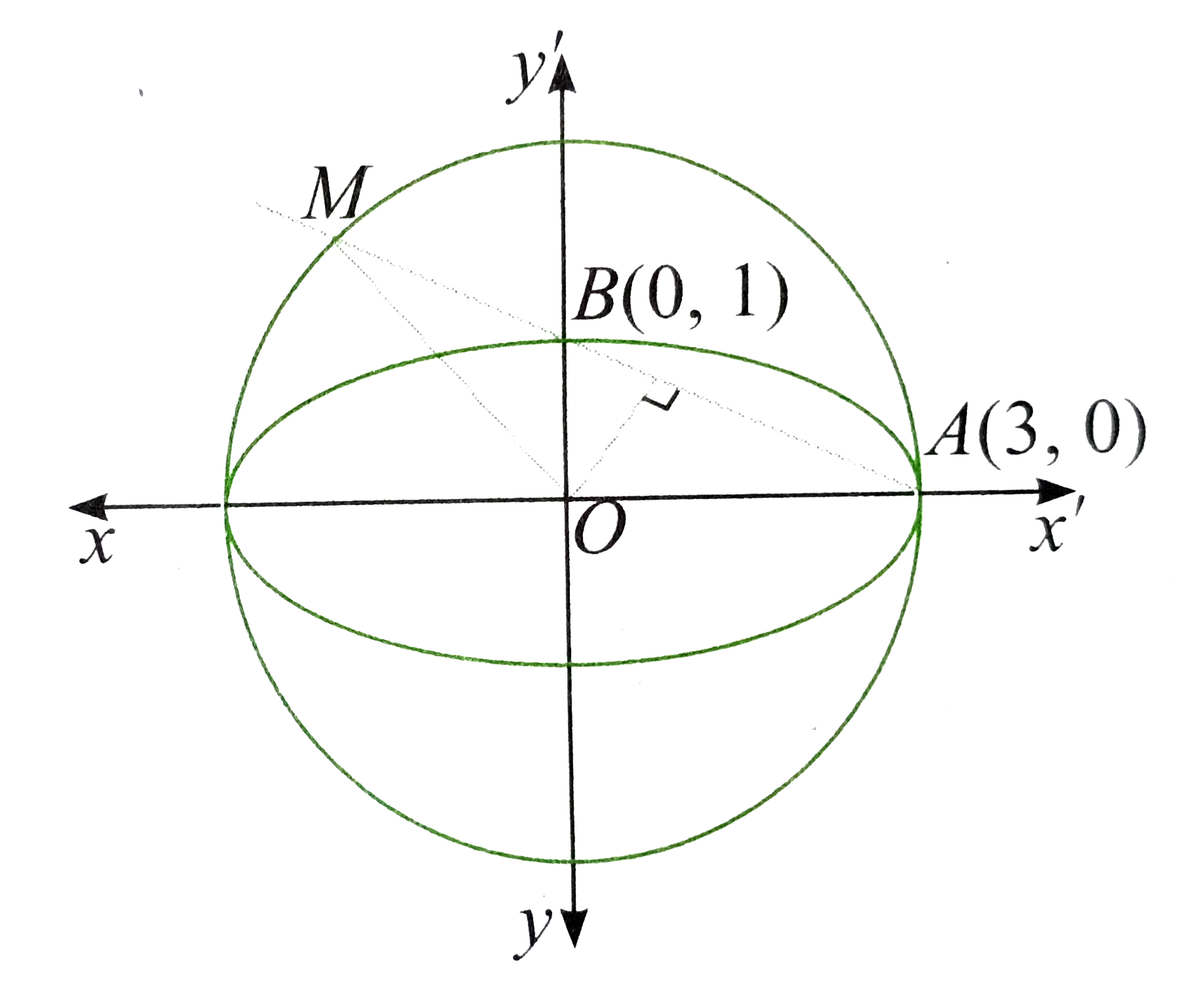
The equation AM is x+3y-3=0
Perpendicualr distacne of line from the origin =3√10=OB
Length of AM=2√(9−910)=2×9√10
∴Area ofΔOAM=12×2×9√10×3√10=2710 sq. units
Similar Questions
दीर्घवृत्त x2+9y2=9 के दीर्घ-अक्ष के सिरे A तथा लघु-अक्ष के सिरे B से गुजरने वाली रेखा इसके सहायक वृत्त को बिन्दु M पर मिलती है, तो शीर्षों A,M एवं मूल बिन्दु O वाले त्रिभुज का क्षेत्रफल है
06:43View SolutionThe line passing through the extremity A of the major exis and extremity B of the minor axis of the ellipse x^2+9y^2=9 meets is auxiliary circle at the point Mdot Then the area of the triangle with vertices at A ,M , and O (the origin) is 31/10 (b) 29/10 (c) 21/10 (d) 27/10
05:50View SolutionIn an ellipse, if the lines joining focus to the extremities of the minor axis form an equilateral triangle with the minor axis, then the eccentricity of the ellipse is
04:36View SolutionThe line passing through the extremity A of the major axis and extremity B of the minor axis of the ellipse x^(2)+9 y^(2)=9 meets the auxiliary circle at the point M. Then the area of the triangle with vertices A, M and the origin O is
05:59View SolutionThe line passing through the extremity A of the major exis and extremity B of the minor axis of the ellipse x^2+9y^2=9 meets is auxiliary circle at the point Mdot Then the area of the triangle with vertices at A ,M , and O (the origin) is (a)31/10 (b) 29/10 (c) 21/10 (d) 27/10
07:07View SolutionThe line passing through the extremity A of the major axis and extremity B of the minor axis of the ellipse x^2 + 9y^2 = 9 meets its auxiliary circle at the point M. Then the area of the triangle with vertices at A,M and the origin O is
04:04View SolutionThe line passing through the extremity A of the major axis and extremity B of the minor axis of the ellipse x^2 +9y^2 = 9 meets its auxiliary circle at the point M. Then the area of the triangle with vertices at A, M, and O (the origin) is
View SolutionThe line passing through the extremity A of the major axis and extremity B of the minor axis of the ellipse x^(2) + 9y^(2)=9 meets its auxiliary circle at the point M. Then, the area of the triangle with vertices at A, M and the origin O is
04:04View Solution

