Question

The line $x=c$ cuts the triangle with corners $(0,0),(1,1)$ and $(9,1)$ into two region. two regions to be the same c must be equal to (A) $\frac{5}{2}$ (B) 3 (C) $\frac{7}{2}$ (D) 5 or 15

Answer

3

Explanation

Area of `DeltaOAB = (1)/(2)(1)(8)` = 4 sq. units

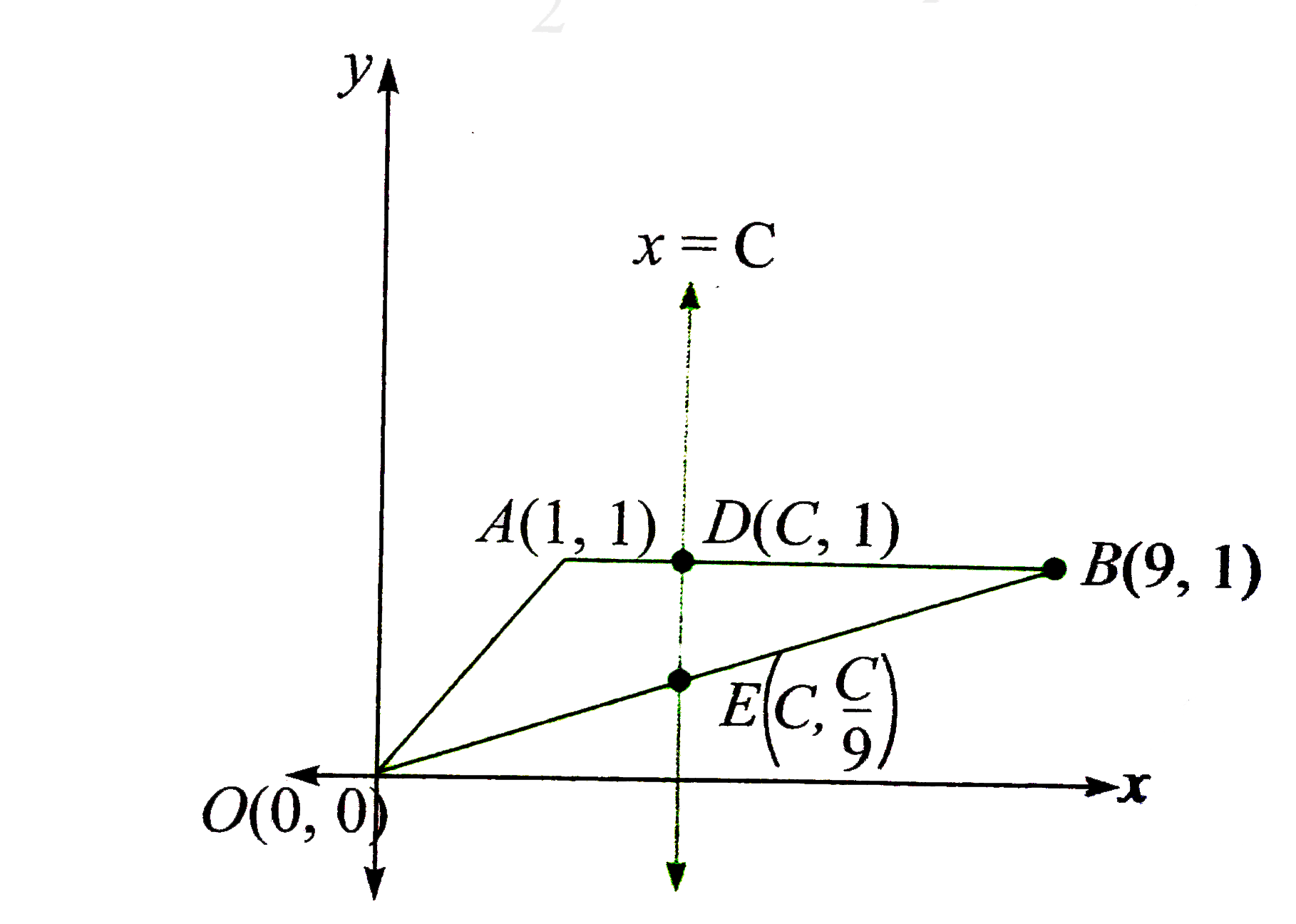
The equation of OB is
`y = (1)/(9)x`
Hence, the point E is (C, C/9).
Now, the area of `Delta BDE` is 2 sq. units. Therefore,
`"or " (1)/(2)(1-(C)/(9))(9-C) = 2`
`"or "(9-C)^(2) = 36`
`"or " 9-C = +-6`
or C=3