The locus of a point on rhombus ABCD, so that it is equidistant from
AB and BC
The correct Answer is:Diagonal BD
To find the locus of a point on rhombus ABCD that is equidistant from sides AB and BC, we can follow these steps:
1. Draw the Rhombus: Start by sketching the rhombus ABCD. Label the vertices A, B, C, and D in a clockwise manner.
2. Draw the Angle Bisector: Draw the angle bisector of angle A (∠A). This line will divide the angle A into two equal angles. Let this bisector intersect side BC at point E.
3. Join Diagonal BD: Draw the diagonal BD of the rhombus. This line will help in finding the intersection point with the angle bisector.
4. Find Intersection Point O: Identify the point O where the diagonal BD intersects the angle bisector AE.
5. Draw Perpendiculars: From point O, draw a perpendicular line OL to side AB and another perpendicular line OM to side AD.
6. Analyze Triangles AOL and AOM: Now, consider triangles AOL and AOM. We will prove that these two triangles are congruent.
7. Congruence of Triangles:
- Angle OAL = Angle OAM (because AE is the angle bisector).
- Angle OLA = Angle OMA = 90° (because OL and OM are perpendiculars).
- OA = OA (common side).
- By the Angle-Angle-Side (AAS) postulate, triangles AOL and AOM are congruent.
8. Conclusion: Since triangles AOL and AOM are congruent, the corresponding parts of these triangles are equal. Thus, OL = OM, which means that point O is equidistant from sides AB and AD.
Therefore, the locus of points that are equidistant from sides AB and BC is the angle bisector of angle A, which is the line AE.
- Angle OAL = Angle OAM (because AE is the angle bisector).
- Angle OLA = Angle OMA = 90° (because OL and OM are perpendiculars).
- OA = OA (common side).
- By the Angle-Angle-Side (AAS) postulate, triangles AOL and AOM are congruent.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(A)26videos
LOCI (LOCUS AND ITS CONSTRUCTIONS)
- BOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions15videos
LINEAR INEQUATIONS
- BOOK - ICSECHAPTER - MATHEMATICS -2014EXERCISE - SECTION- B29videos
MATHEMATICS -2014
Similar Questions
Knowledge Check
- Question 1 - Select One
The locus of the point which is equidistant from the point A(0,2,3)andB(2,−2,1) is
Ax - 2y - z + 1 = 0Bx + 2y - z - 1 = 0Cx + 2y + z + 1 = 0DNone of these
AB is a chord of a circle. Draw the locus of a point in the circle so that it is equidistant from A and B.
View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that :
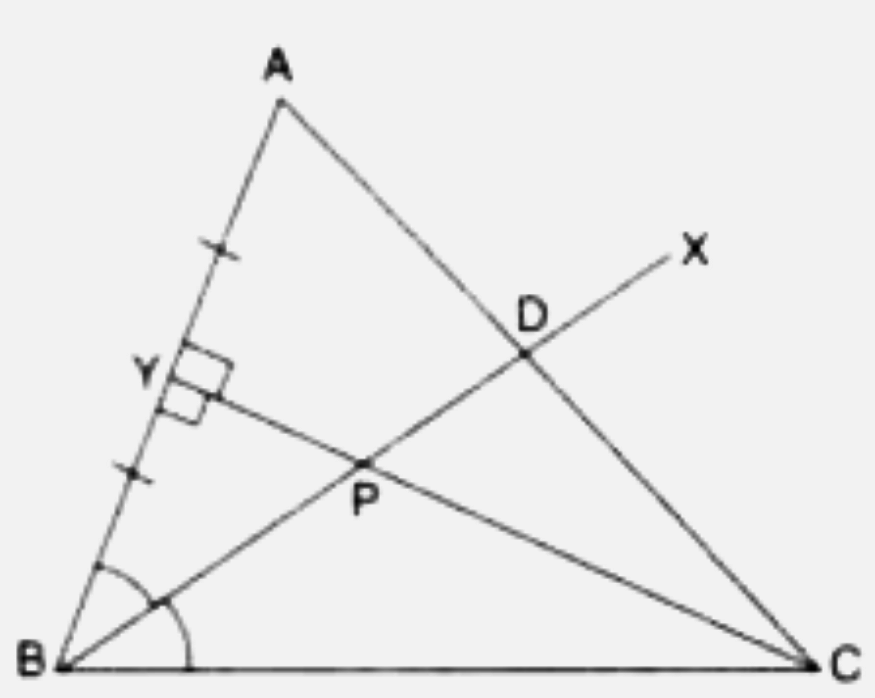
point D is equidistant from AB and BC.View SolutionUsing ruler and a compass only, construct a semi-circle with diameter BC = 7 cm. Locate a point A on the circumference of the semi-circle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure ∠ADC and write it down.
View SolutionFind the locus of a point whose each point is equidistant from the points A(2,3,-4) and B(-1,2,3).
View SolutionUse ruler and compasses only for this question
Construct the locus of points inside the triangle which are equidistant from B and C.View SolutionConstruct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC=60∘. Locate by construction the point P such that :
P is equidistant from AB and BC.
Measure and record the length of PB.View SolutionUsing ruler and compass only, construct a ΔABC such that BC = 5 cm and AB = 6.5 cm and ∠ABC=120∘.
(i) Construct a circumference of ΔABC
(ii) Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and BC.View Solution
