The maximum value of z = 10x + 6y subject to constraints x≥0,y≥0,x+y≤12,2x+y≤20 is
A
72
B
80
C
104
D
110
Video Solution
Text Solution
The correct Answer is:C
Given , Z= 10x +6y and constriants are
x≥0
y≥0
x+y≤12,and2x+y≤20
The feasible region is OABCO.
∴ Maximum of z must occurs of the correct points of the feasible reagain .
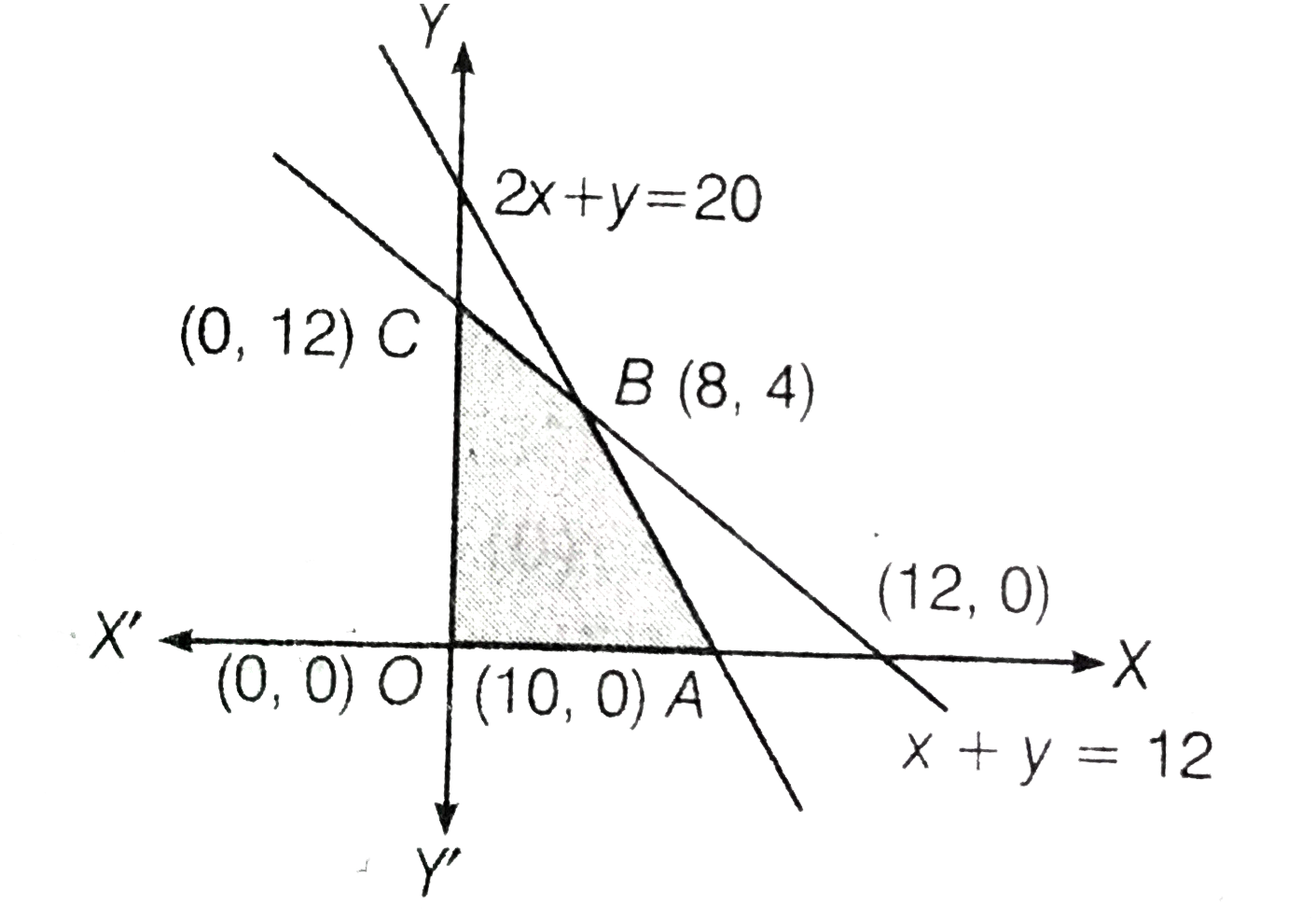
Hence , maximum vlaue of Z is 104

GIven objective function is Z =3x -4y .

|
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Knowledge Check
The maximum value of Z=10x+6y subject to constraints x≥0,y≥0,x+y≤12,2x+y≤20, is
A72B80C104D110Maximum value of Z = 12x + 3y subject to constraints x≥0,y≥0,x+y≤5 and 3x+y≤9 is
A15B36C60D40Maximum value of Z = 12x + 3y subject to constraints x≥0,y≥0,x+y≤5 and 3x+y≤9 is
A15B36C60D40
The maximum value of Z=3x+5ysubjected to the constraints x+y≤2,4x+3y≤12,x≥0,y≥0 is
View SolutionThe minimum value of P = 6x + 16y subject to constraints x≤40,y≤20 and x,y≥0 is
View SolutionThe point at which the minimum value of z=8x+12y subject to the constraints 2x+y≥8,x+2y≥10x≥0,y≥0 is obtained is
View SolutionThe point at which the maximum value of Z=4x+6y subject to the constraints 3x+2y≤12,x+y≥4,x≥0,y≥0 is obtained at the point
View SolutionThe maximum value of Z=3x+4y subject to the constraints:
x+y≤4,x≥0,y≥0 is :
View Solution
