The measure of one angle of a parallelogram is What are the measures of the remaining angles?
To find the measures of the remaining angles of a parallelogram when one angle is given as 70∘, we can follow these steps:
Step 1: Identify the given angle
Let’s denote the given angle as A. So, we have:
A=70∘
Step 2: Use the property of adjacent angles in a parallelogram
In a parallelogram, adjacent angles are supplementary, which means they add up to 180∘. Therefore, we can find the adjacent angle B using the formula:
A+B=180∘
Step 3: Calculate the adjacent angle
Substituting the value of A into the equation:
70∘+B=180∘
To find B, we rearrange the equation:
B=180∘−70∘
B=110∘
Step 4: Find the opposite angles
In a parallelogram, opposite angles are equal. Thus, we can find the measures of the remaining angles:
- The angle opposite to A (which we can denote as C) is equal to A:
C=A=70∘
- The angle opposite to B (which we can denote as D) is equal to B:
D=B=110∘
Step 5: Summarize the angles
Now we have all the angles of the parallelogram:
- Angle A=70∘
- Angle B=110∘
- Angle C=70∘
- Angle D=110∘
Final Answer:
The measures of the angles in the parallelogram are:
- 70∘,110∘,70∘,110∘
---
Let’s denote the given angle as A. So, we have:
A=70∘
In a parallelogram, adjacent angles are supplementary, which means they add up to 180∘. Therefore, we can find the adjacent angle B using the formula:
A+B=180∘
Substituting the value of A into the equation:
70∘+B=180∘
To find B, we rearrange the equation:
B=180∘−70∘
B=110∘
In a parallelogram, opposite angles are equal. Thus, we can find the measures of the remaining angles:
- The angle opposite to A (which we can denote as C) is equal to A:
C=A=70∘
- The angle opposite to B (which we can denote as D) is equal to B:
D=B=110∘
Now we have all the angles of the parallelogram:
- Angle A=70∘
- Angle B=110∘
- Angle C=70∘
- Angle D=110∘
The measures of the angles in the parallelogram are:
- 70∘,110∘,70∘,110∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
The measure of one of the parallelogram is 70∘. Find the measures of the angles of the parallelogram .
The following steps are involved in solving the above problem. Arrange them in sequential order.
(A) 70∘+x=180∘⇒x=110∘
(B) Let the angle adjacent to 70∘ be x.
(C ) The sum of the measures of adjacent angle of a parallelogram is 180∘.
(D) The measure of the angles of the parallelogram are 70∘,110∘,70∘and110∘ACBDABBCADCBCDADCDABIf the smaller angle of a parallelogram is 30∘ , then the measure of the bigger angle is
A60∘B150∘C180∘D360∘The measure of one of the parallelogram is 70∘. Find the measures of the angles of the parallelogram .
The following steps are involved in solving the above problem. Arrange them in sequential order.
(A) 70∘+x=180∘⇒x=110∘
(B) Let the angle adjacent to 70∘ be x.
(C ) The sum of the measures of adjacent angle of a parallelogram is 180∘.
(D) The measure of the angles of the parallelogram are 70∘,110∘,70∘and110∘ACBDABBCADCBCDADCDAB
Two adjacent angles of a parallelogram are equal. What is the measure of each?
View SolutionThe angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is
View SolutionWhat is the measure of ∠DBC?
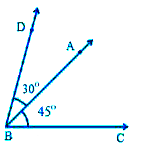
View SolutionThe measures of two adjacent angles of a parallelogram are in the ratio 3:2. Find the measure of each of the angles of the parallelogram.
View SolutionThe measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
View Solution
