The minimum value of 2x2+x−1 is

A

−14

B

34

C

−98

D

94

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

We know that for a>0,y=ax2+bx+c has minimum value equal to −(b2−4ac)4a
Here, a = 2, b=1 and c = -1.
So, the minimum value of 2x2+x−1is−(1+88)=−98
Now, let α be a root of the quadratic equation ax2+bx+c=0. Then, aα2+bα+c=0⇒Point(α,0)lies ony=ax2+bx+c=0
It follows from this that every real root of ax2+bx+c=0 is represented by the point of intersecton of the parabola with x-axis and vice-versa.
Thus, we may draw the following conclusions:
(I) The parabola will intersect the x-axis in two distinct points iff D > 0.
In this case, the parabola meets x-axis at (α,0)and(β,0) where
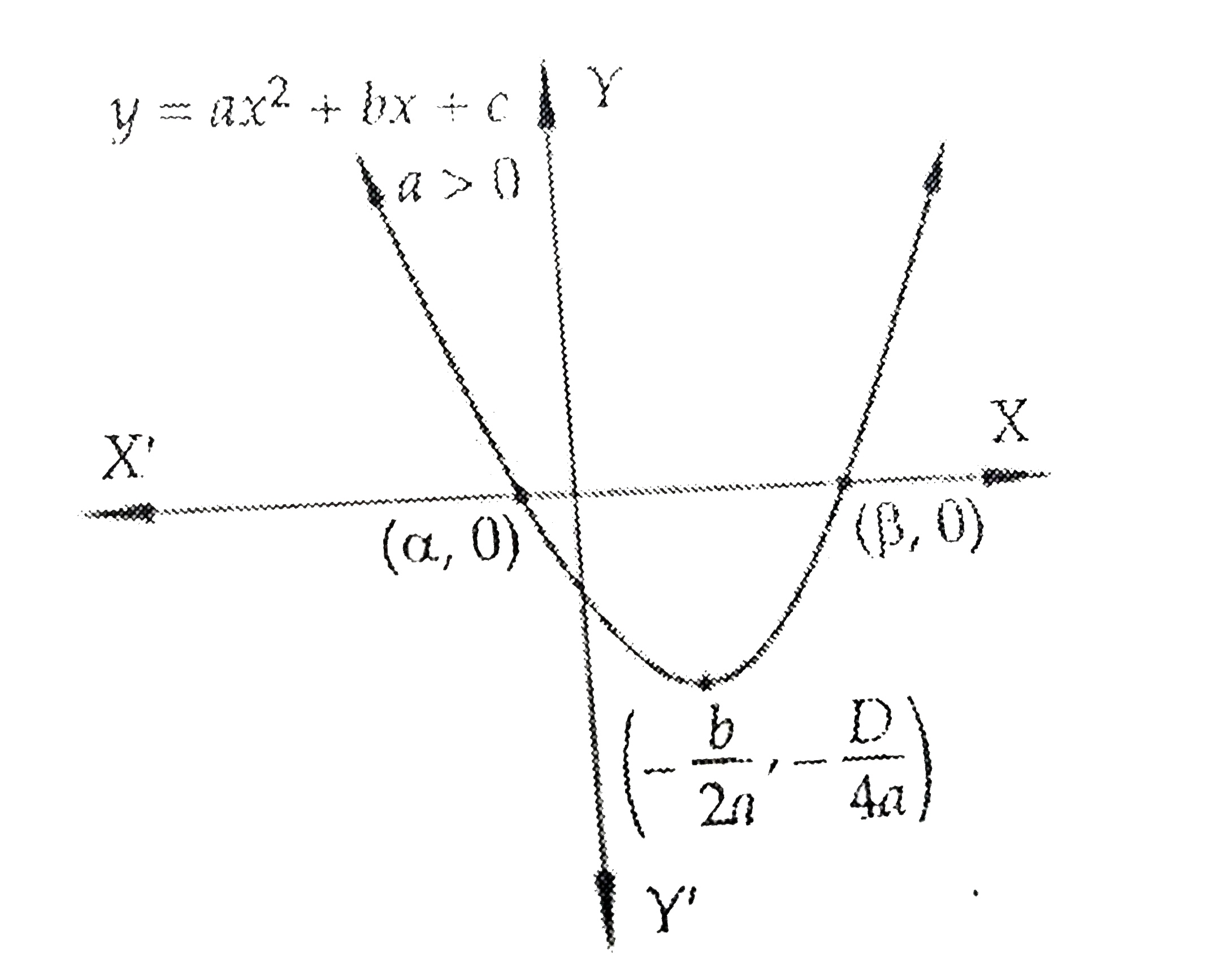
ocr_image
For a > 0, we have
ymin=−D4aat x=−b2a,ymax→∞
and, y=f(x)⎧⎪⎨⎪⎩<0for<α<x<β=0forx=α,β>0forx<αorx>β
For a < 0, we have
ymax=−D4aat x=−b2a,ymin→−∞
and, y=f(x)⎧⎪⎨⎪⎩<0forx<αorx>β=0forx=α,β>0forα<x<β
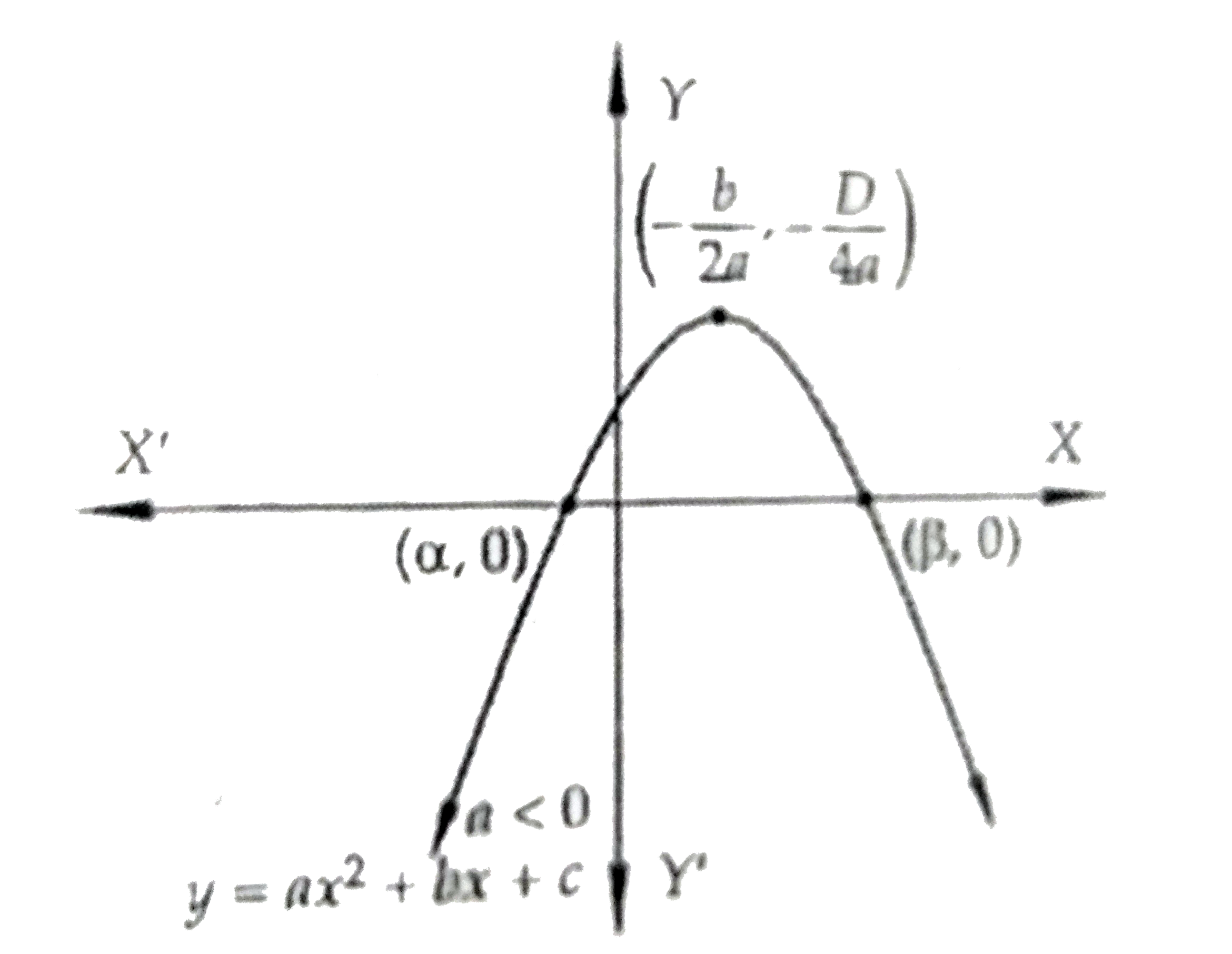
ocr_image
(II) The parabola will just touch the x-axis at one point iff D = 0 In this case, the parabola touches x-axis at (α,0), where
ocr_image
For a > 0, we have
ymin=−D4aat x=−b2a,ymax→∞
and, y=f(x){>0for x≠α=0for x=α
For a < 0, we have
ymax=0at x=−b2a,ymin→−∞
and, y=f(x){<0for x≠α=0for x=α
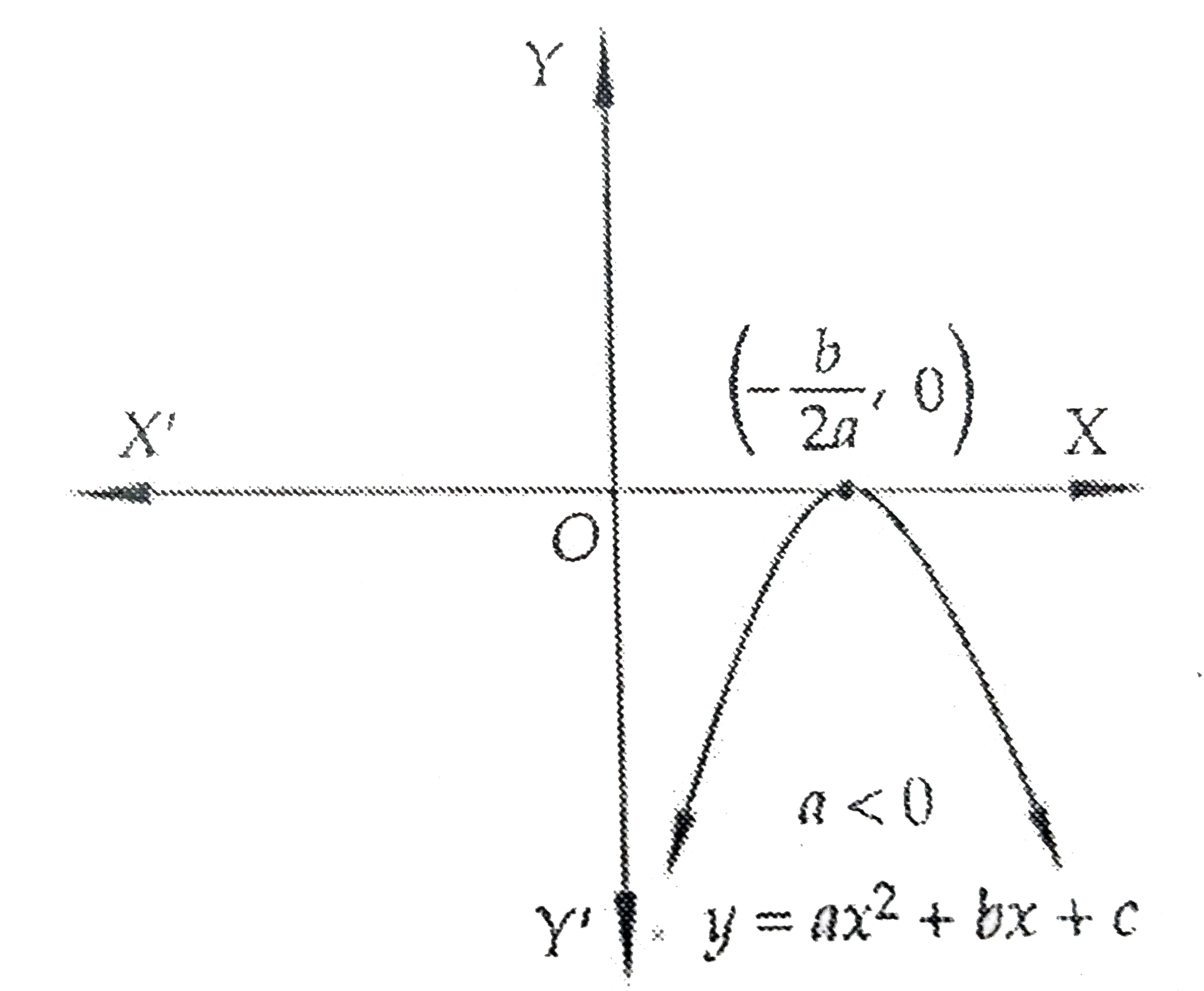
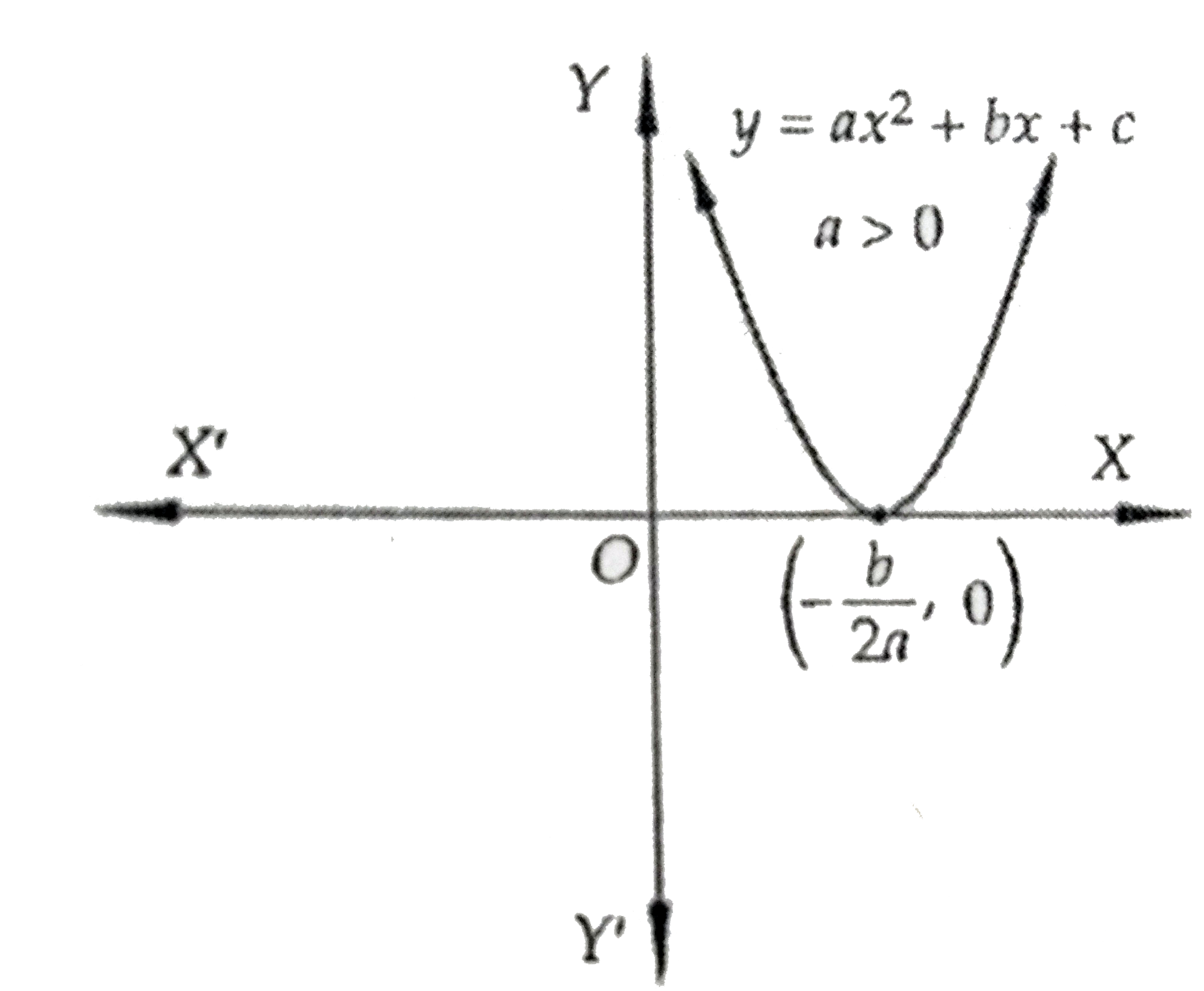
ocr_image
(III) The parabola will not intersect x-axis iff D < 0
In this case, the parabola remains either completely above x-axis or completely below x-axis according as a>0ora<0.
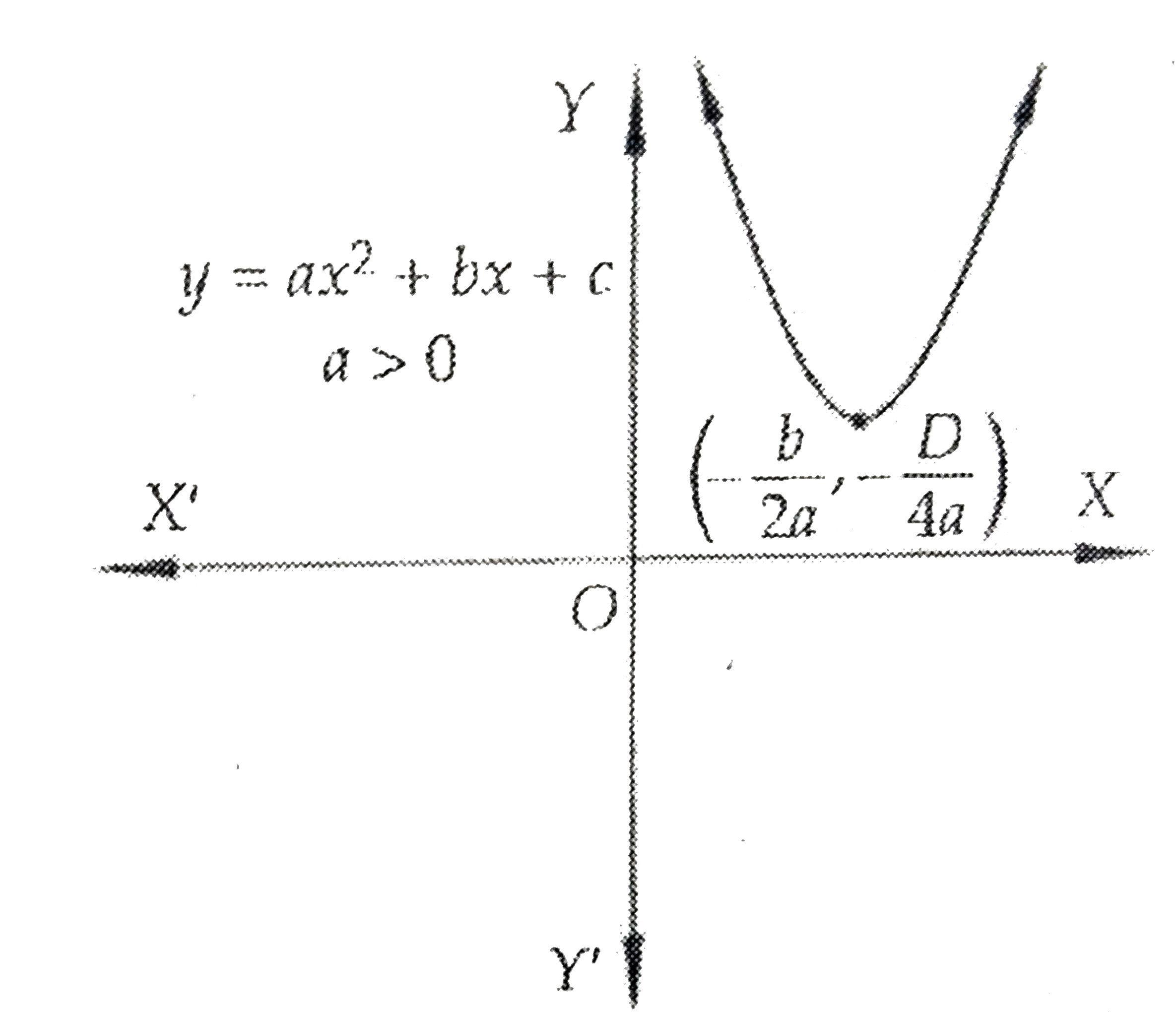
ocr_image
For a > 0, we have
ymin=−D4aat x=−b2a, ymax→∞
For a < 0, we have
ymax=−D4aat x=−b2a,ymin→−∞
and, y=f(x)<0 for all x
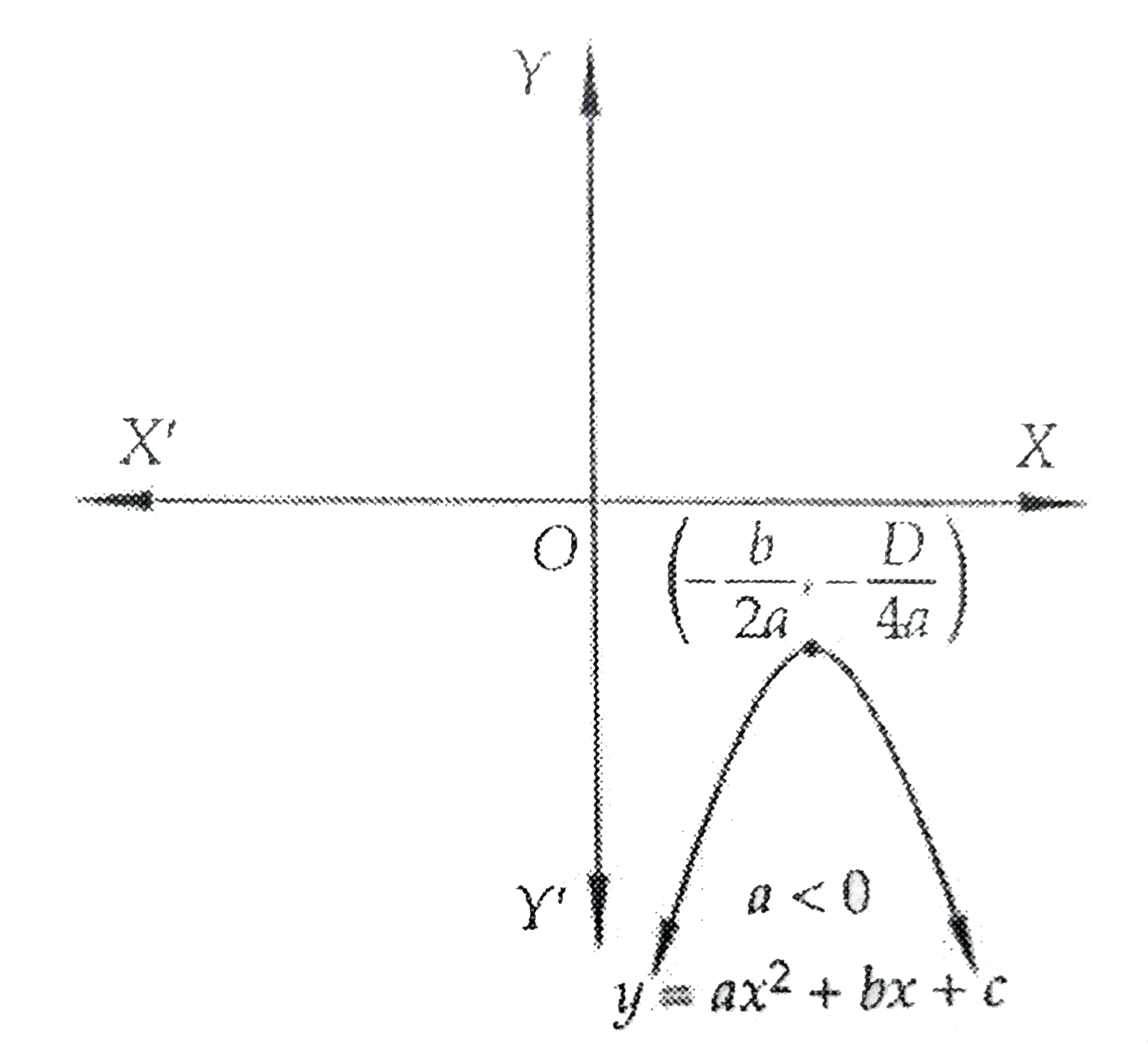
ocr_image
If follows from the above discussion that, for real values of x, the sign of the quadratic expression f(x)=ax2+bx+c is same as that of 'a', except when the roots of the equation ax2+bx+c=0 are real and distinct and x lies between them.
It also follows that ax2+bx+c>0 for all x∈R iff a>0andD<0,
and, ax2+bx+c<0 for all x∈R iff a<0andD<0.

Updated on:21/07/2023
|