Doubtnut Promotions Sticky

The minimum value of the objective function Z=2x+10y for linear constraints x≥0,y≥0,x−y≥0,x−5y≤−5 is

A

10

B

15

C

12

D

8

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Given Z=2x +10 y
Here, feasible region is undbounded .
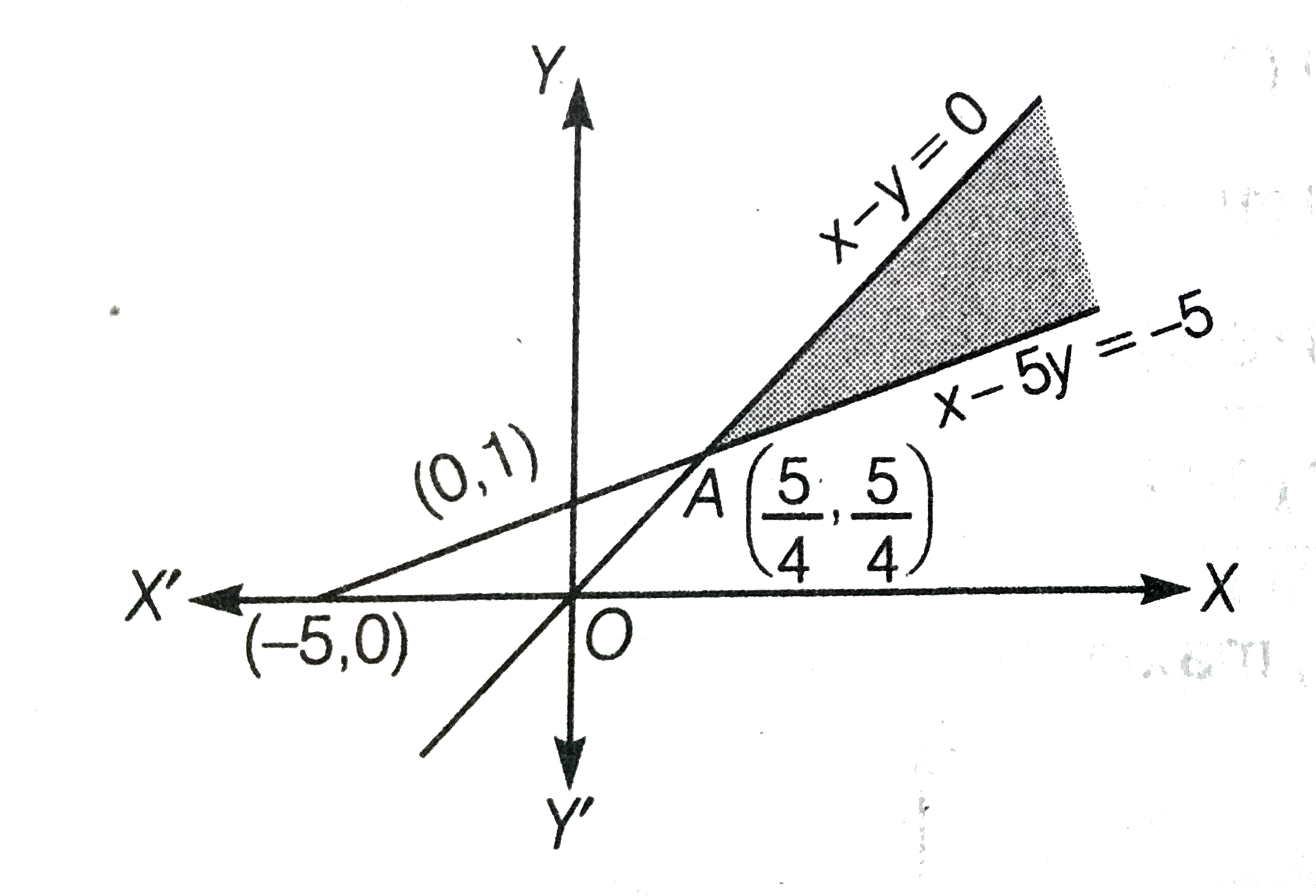
ocr_image
At point A(54,54),Z=2(54)+10(54)=15
Now, this value of Z may be minimum value. We see that half plane determined by 2x + 1 Oy lt 15 has no point in common with the feasible region . So, Z has minimum value 15.

|
Updated on:21/07/2023
Class 12MATHSLINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The maximum value of the objective function Z=3x+2y for linear constraints x+y≤7,2x+3y≤16,x≥0,y≥0 is

    A16
    B21
    C25
    D28
  • Question 2 - Select One

    The minimum and maximum values of the objective function, Z = 5x + 10y subject to the constraints x+2y≤120,x+y≥60,x−2y≥0,x,y≤0 are respectively

    A300 and 500
    B600 and 700
    C600 and 700
    D300 and 400
  • Question 3 - Select One

    The minimum value of the objective function Z=x+2y
    Subject to the constraints,
    2x+y≥3,x+2y≥6,x,y≥0 occurs

    Aat every point on the line x + 2y = 6
    Bat every point on the line 2x + y = 3
    Cat every point on the line x + 2y = 3 d
    Dat every point on the line 2x + y = 6