Question

The number of points in $(-\infty ,\infty ),$
for which $x^2-x\sin x-\cos x=0,$
is
6 (b)
4 (c) 2
(d) 0

Options

A. 6
B. 4
C. 2
D. 0

Answer

C

Explanation

We have to find the number of solution of the equation
`x^(2)-xsin x-cos x=0" or ",x^(2)=xsinx+cosx`
Let f(x)`=x^(2)` and g(x)`=xsin x+cos x`
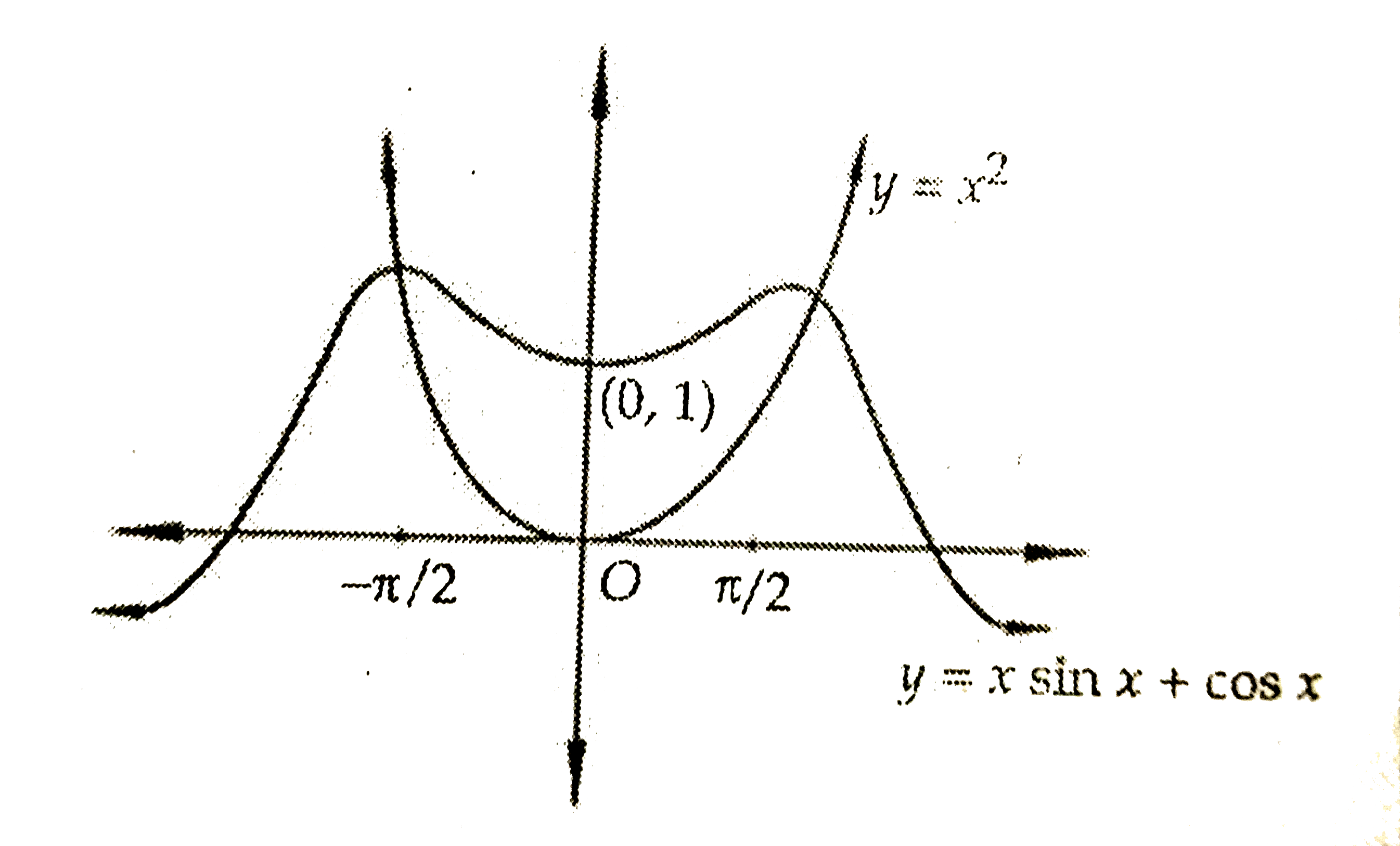
Clearly, the numbers of solutions of the curves y=f(x) and y=g(x). The curve y=f(x) is a parabola with vertex at (0,0) and y-axis as axis of symmetry.
Now,g(x)=xsinx+cosx
`rArr g'(x)=xcosx`
The changes in signs of g'(x) are shown in the Figure 16.

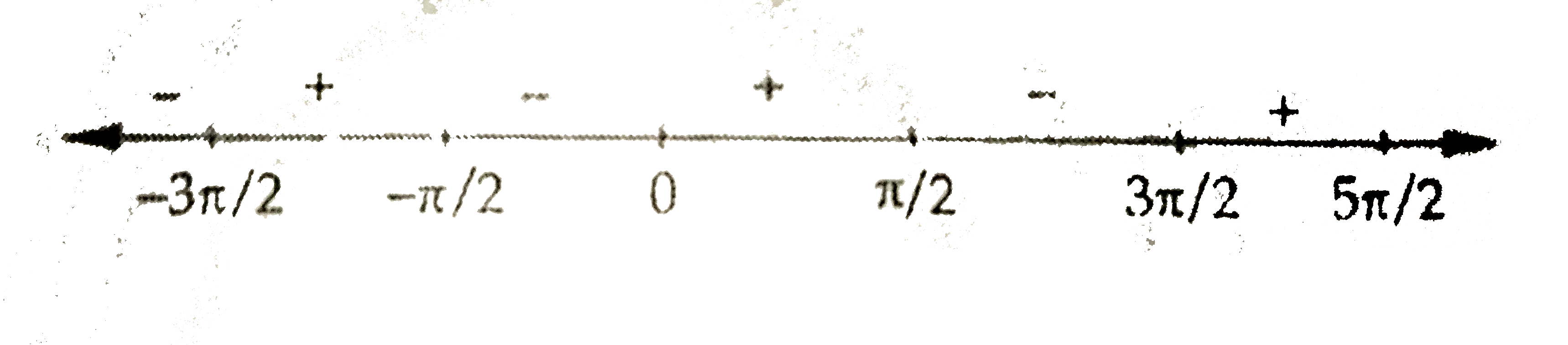
Clearly, `x=0,(3pi)/(2)` are points of relative minima and `x=+-(pi)/(2),x=(5pi)/(2)` etc are points of relative maxima. Also, g(x)`=xsinx+cosx` is an even function and g(0)=1, `g(pi//2)=pi//2` and `g(pi)=-1`. So, a rough sketch of y=g(x) is as shown in Figure 17.
Clearly, y=f(x) and y=g(x) intersect at two points.
Hence, given equation has two solutions.