The number of rectangles excluding squares from a rectangle of size 11×8 is 48λ, then the value of λ is
13
23
43
53
The correct Answer is:C
Step by step video & image solution for The number of rectangles excluding squares from a rectangle of size 11xx8 is 48lamda, then the value of lamda is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise For Session 7
5 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Single Option Correct Type Questions)
30 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise For Session 5
18 Videos
- PARABOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
36 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
Similar Questions
Knowledge Check
In the figure, the area of rectangle EFGH is 3 units greater than the area of rectangle ABCD. What is the value of ab if a+b=8 ?
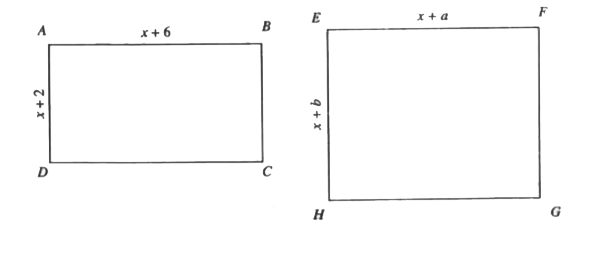 A9B12C15D18
A9B12C15D18
The area of a rectangle of size 1.23×2.345cm is
View SolutionFind number of rectangles in a chessboard, which are not a square.
View SolutionIf the difference of the roots of x2−λx+8=0 be 2 the value of λ is
View SolutionThe mean deviation about mean of the data 2,3,7,11,13,17,2,1isλ8 then value of λ is
View SolutionIf number of ways in which 7 different balls can be distributed into 4 boxes, so that no box remains empty is 48λ, the value of λ is
View SolutionIf number of ways in which 7 identical balls can be distributed into 4 boxes, so that no box remains empty is 4λ, the value of λ is
View SolutionThe plane x−y−z=2 is rotated through 90∘ about its line of intersection with the plane x+2y+z=2. The distance of (−1,−2,−1) from the plane in the new position is λ√67. Then the value of λ is equal to
View Solution