The number of solutions of tanx−mx=0,m>1, in (−π2,π2) is 1 (b) 2 (c) 3 (d) mSolution in Bengali
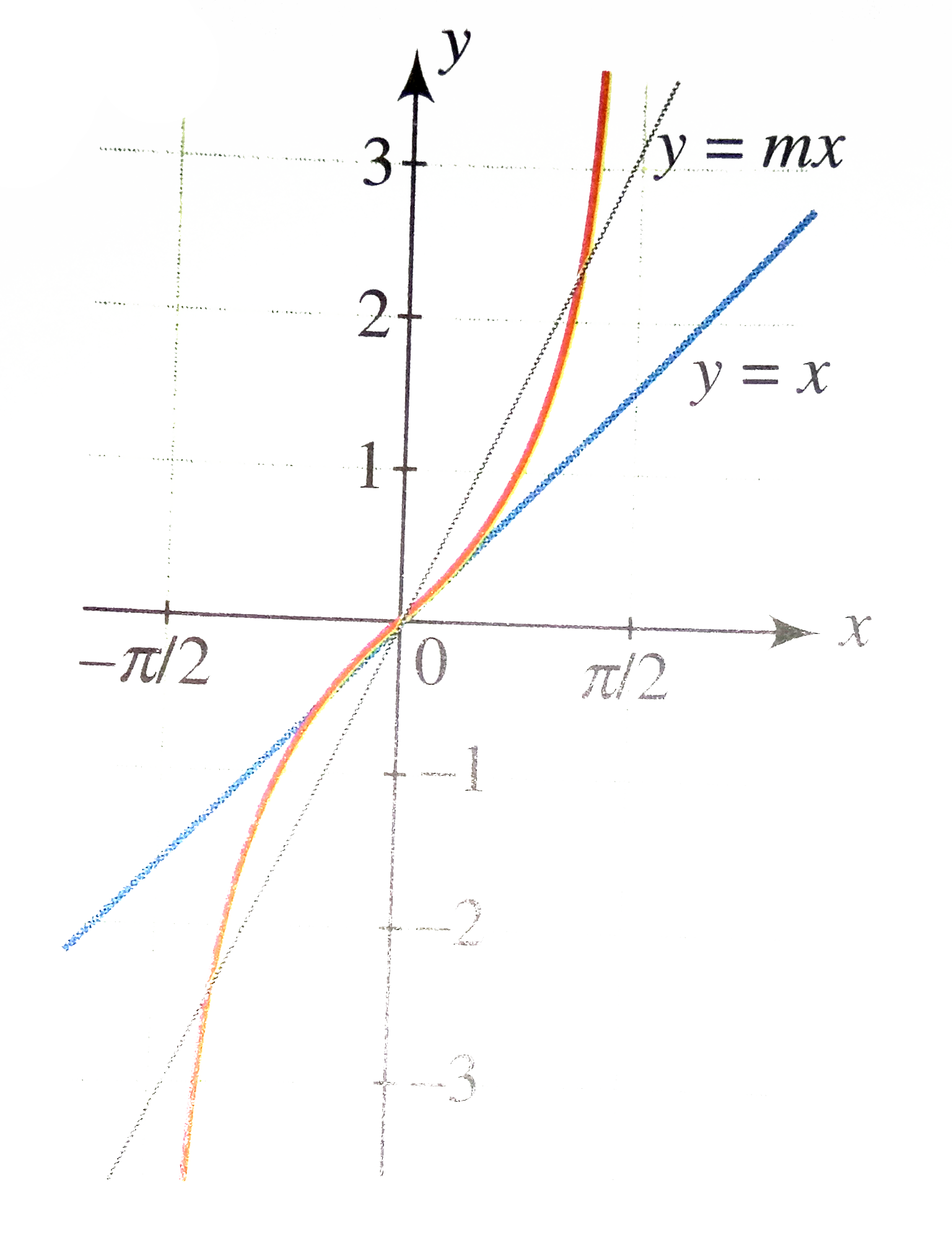
In (−π2,0), the graph of y = tan x lies below the line y = x, which is the tangent at x = 0 and in (0,π2), it lies above the line y = x.
For m>1, the line y = mx lies below y = x in (−π2,0) and above y = x in (0,π2). The graphs of y = tan x and y = mx, m>1, meet at three points,
including x = 0 in (−π2,π2).
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of y=1(1/x).
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionFor 0<θ<π2 , the solution (s) of
6∑m=1cosec(θ+(m−14)cosec(θ+mπ4)4√2 is/are.
View SolutionThe number of solution of equation sin−1x+nsin−1(1−x)=mπ2,wheren>0,m≤0, is 3 (b) 1 (c) 2 (d) None of these
View SolutionThe number of solutions of tanx−mx=0,m>1, in (−π2,π2) is (A) 1 (B) 2 (C) 3 (D) m
View Solutionthe number of solutions of cos^(-1)(1-x)+m cos^(-1)x=(n pi)/(2) where m>0,n<=0
View SolutionIf f(x)={mx+1 , x≤π2, sinx+n , x>π2 is continuous at x=π2 , then m=1, n=0 (b) m=nπ2+1 (c) n=mπ2 (d) m=n=π2
View SolutionIf equation x2−(2+m)x+1(m2−4m+4)=0 has coincident roots then (A) m=0,m=1 (B) m=0,m=2 (C) m=23,m=6 (D) m=23,m=1
View Solution∫π/20tanx1+m2tan2x dx
View Solution∫π/20tanx1+m2tan2x dx
View SolutionThe number of solutions of the equation tan^(-1)(1+x)+tan^(-1)(1-x)=pi/2 is 2 (b) 3 (c) 1 (d) 0
View SolutionThe number of solutions of tanx−mx=0,m>1, in (−π2,π2) is (A) 1 (B) 2 (C) 3 (D) m
View SolutionDifferentiate tan−1(tanx), x∈[0, π]−{π2}
View Solutioncos^(-1) (1 - x) + m cos^(-1)x = (n pi)/(2), m gt 0, n lt 0 The total number of solutions will be
View SolutionIf 0<θ<π/2, number of solutions of 6∑m=1cosec(θ+(m−1)π4)cosec(θ+mπ4)=4√2 is
View Solution
