The ordinate and the normal at any point P on the curve meet the x-axis at points A and B respectively. Find the equation of the family of curves satisfying the condition , The product of abscissa of P and AB=arithmetic mean of the square of abscissa and ordinate of P.
To solve the problem, we need to find the equation of the family of curves that satisfy the given condition. Let's break down the solution step by step.
Step 1: Understand the Problem
We have a point P(x,y) on the curve. The ordinate (y-coordinate) and the normal at point P meet the x-axis at points A and B respectively. We need to find the equation of the family of curves where the product of the abscissa of P and the length AB equals the arithmetic mean of the squares of the abscissa and ordinate of P.
Step 2: Define Points A and B
1. Point A: Since A is where the ordinate meets the x-axis, it has coordinates (x,0).
2. Point B: The normal at point P meets the x-axis at point B. The equation of the normal can be derived from the slope of the tangent at point P.
Step 3: Equation of the Normal
The slope of the tangent at point P is given by dydx. The slope of the normal will be −dxdy. The equation of the normal line at point P(x,y) can be written as:
y−y1=−dxdy(x−x1)
Substituting (x1,y1)=(x,y):
y−y=−dxdy(x−x)
This simplifies to:
y=−dxdy(x−x)+y
Step 4: Finding the Coordinates of B
Setting y=0 in the normal equation gives us the x-coordinate of point B:
0−y=−dxdy(X−x)
Thus,
X=x+ydxdy
Step 5: Length of AB
The length AB can be calculated as:
AB=X−x=ydxdy
Step 6: Set Up the Condition
According to the problem, we have:
x⋅AB=x2+y22
Substituting for AB:
x⋅⎛⎜⎝ydxdy⎞⎟⎠=x2+y22
This simplifies to:
xydxdy=x2+y22
Step 7: Rearranging the Equation
Rearranging gives:
dydx=2xyx2+y2
Step 8: Substitute y=vx
Let y=vx, then dydx=v+xdvdx. Substituting this into the equation gives:
v+xdvdx=2x(vx)x2+(vx)2
This simplifies to:
v+xdvdx=2vx2x2(1+v2)=2v1+v2
Step 9: Solve the Differential Equation
Rearranging and separating variables leads to:
2v1−v2dv=dxx
Integrating both sides gives:
∫2v1−v2dv=∫dxx
This results in:
−log(1−v2)=log(x)+C
Step 10: Final Equation
Exponentiating gives:
1−v2=Cx
Substituting back v=yx:
1−y2x2=Cx
Rearranging leads to:
x2−y2=Cx
This is the required equation of the family of curves.
We have a point P(x,y) on the curve. The ordinate (y-coordinate) and the normal at point P meet the x-axis at points A and B respectively. We need to find the equation of the family of curves where the product of the abscissa of P and the length AB equals the arithmetic mean of the squares of the abscissa and ordinate of P.
1. Point A: Since A is where the ordinate meets the x-axis, it has coordinates (x,0).
2. Point B: The normal at point P meets the x-axis at point B. The equation of the normal can be derived from the slope of the tangent at point P.
The slope of the tangent at point P is given by dydx. The slope of the normal will be −dxdy. The equation of the normal line at point P(x,y) can be written as:
y−y1=−dxdy(x−x1)
Substituting (x1,y1)=(x,y):
y−y=−dxdy(x−x)
This simplifies to:
y=−dxdy(x−x)+y
Setting y=0 in the normal equation gives us the x-coordinate of point B:
0−y=−dxdy(X−x)
Thus,
X=x+ydxdy
The length AB can be calculated as:
AB=X−x=ydxdy
According to the problem, we have:
x⋅AB=x2+y22
Substituting for AB:
x⋅⎛⎜⎝ydxdy⎞⎟⎠=x2+y22
This simplifies to:
xydxdy=x2+y22
Rearranging gives:
dydx=2xyx2+y2
Let y=vx, then dydx=v+xdvdx. Substituting this into the equation gives:
v+xdvdx=2x(vx)x2+(vx)2
This simplifies to:
v+xdvdx=2vx2x2(1+v2)=2v1+v2
Rearranging and separating variables leads to:
2v1−v2dv=dxx
Integrating both sides gives:
∫2v1−v2dv=∫dxx
This results in:
−log(1−v2)=log(x)+C
Exponentiating gives:
1−v2=Cx
Substituting back v=yx:
1−y2x2=Cx
Rearranging leads to:
x2−y2=Cx
This is the required equation of the family of curves.
Similar Questions
The tangent at any point P of a curve C meets the x-axis at Q whose abscissa is positive and OP=OQ,O being the origin, the equation of curve C satisfying these conditions may be
View SolutionFind the equation of the curve passing through origin if the slope of the tangent to the curve at any point (x,y)is equal to the square of the difference of the abscissa and ordinate of the point.
View SolutionFind the equation of the curve passing through origin if the slope of the tangent to the curve at any point (x,y)is equal to the square of the difference of the abscissa and ordinate of the point.
View SolutionUse the graph given alongside, to find the co-ordinate of the point (s) satisfying the given condition:
the ordinate is half of the abscissa.
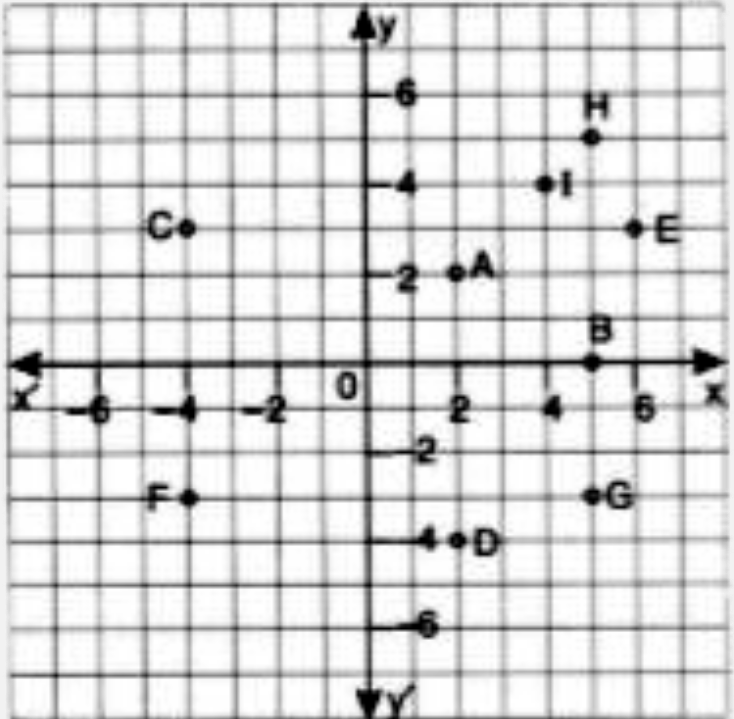
View SolutionUse the graph given alongside, to find the co-ordinate of the point (s) satisfying the given condition:
the abscissa is 5.
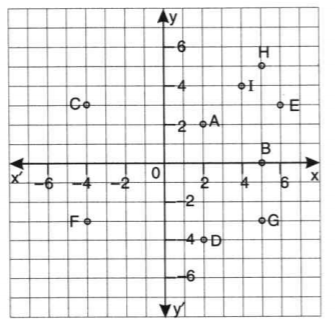
View SolutionUse the graph given alongside, to find the co-ordinate of the point (s) satisfying the given condition:
the abscissa is 2.

View SolutionIf the tangent at any point P of a curve meets the axis of ΞnT. find the curve for which OP=PT,O being the origin.
View SolutionFind the equation of the curve which is such that the area of the rectangle constructed on the abscissa of and the initial ordinate of the tangent at this point is a constanta =a2.
View SolutionIf the length of the portion of the normal intercepted between a curve and the x-axis varies as the square of the ordinate, find the equation of the curve.
View SolutionThe equation of the tangent to the curve y=√9−2x2 at the point where the ordinate & the abscissa are equal is
View Solution