The point (4,1) undergoes the following three transformations successively
(a) Reflection about the line y=x
(b)Translation through a distance 2 units along the positive direction of the x-axis
( c) Rotation through an angle π/4 about the origin in the anti clockwise direction.
The final position of the point is given by the co-ordinates Solution in Bengali
Reflection of P(4,1) about the line y=x is Q(1,4). On translation of Q(1,4) through a distance of 2 units strong positive direction of x-axis, the point moves to R(1+2,4) or R(3,4).
On rotation about origin through an angle of π/4, the point R takes the position S such that OR=OS=5.
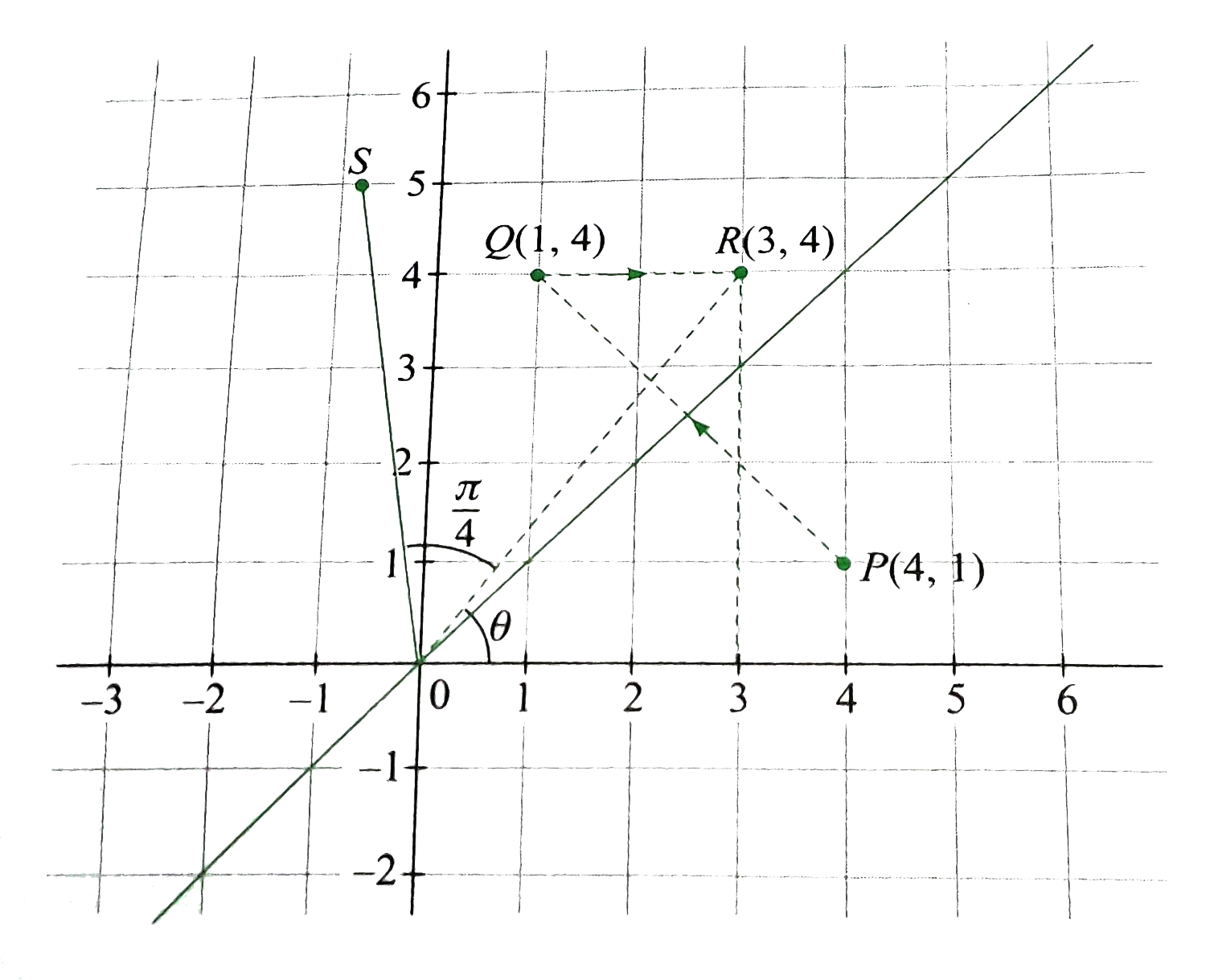
From the figure, cosθ=(35) and sinθ=(45) form trigonometric concepts, coordinates of point S are :
(5cos(π4+θ),=5(π4+θ))
Now , 5cos(π4+θ)=5(cosπ4cosθ−sinπ4sinθ)
=5(1√2.15−1√2.45)=−1√2
and 5sin(π4+θ)=5(sinπ4cosθ+sinθcosπ4)
(1√2.15+1√2.45)=7√2
Coordinates of S are (−1√2,7√2).
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.3
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.4
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main
6 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
At what point should the origin be shifted if the coordinates of a point (4,5) become (−3,9)?
View SolutionIf the axes are shifted to the point (1,−2) without rotation, what do the following equations become? 2x2+y2−4x+4y=0 , y2−4x+4y+8=0
View SolutionThe lines p(p2+1)x−y+q=0 and (p2+1)2x+(p2+1)y+2q=0 are perpendicular to a common line for
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionThe point A(4, 1) undergoes following transformations successively:reflection about line y=x translation ,through a distance of 3 units in the positive direction of x-axis(iii) rotation through an angle 105^@ in anti-clockwise direction about origin O.Then the final position of point A is
View SolutionThe point (1,3) undergoes the following transformations successively (i) Reflection with respect to the line y=x (ii) translation through 3 units along the positive direction of the X-axis (ii) Rotation through an angle (pi)/(6) about the origin in the clockwise direction. The final position of the point P is
View SolutionThe point (4,1) undergoes the following three successive transformations ,
reflection about the line y=x−1
translation through a distance 1 unit along the positive direction
rotation thrpough an angle π4 about the origin in the anti - clockwise direction
Then the coordinates of the final point are ,
View SolutionThe point P(1,3) undergoes the following transformations successively :
(i) Reflection with respect to the line y = x
(ii) Translation through 3 units along the positive direction of the X-axis
(iii) Rotation through an angle of π6 about the origin in the clockwise direction. The final position of the point P is
View SolutionThe point (4,1) undergoes the following transformations successively
I. Reflection about the line y=x
II. Translation through a distance 2 units in the direction of positive X-axis.
III. Rotation through an angle π4 about origin in the anticlock wise direction.
Then, the final position of the point is
View SolutionThe point P(3,2) undergoes the following transformations successively
(i) Reflection about the line y=x
(ii) Translation to a distance of 3 units in the positive direction of X-axis
(iii) Rotation through an angle π4 about the origin in the anti-clockwise direction
Then , the final position of that point is
View SolutionThe point (4, 1) undergoes the following three transformations successively:
(i) reflection about the line y = x (ii) translation through a distance of 2 units along the positive direction of x-axis (ii) rotation through an angle of π4 about the origin in the counter-clockwise direction. The final position of the point is given by:
View SolutionThe point (3, 2) undergoes the following transformations successively
(i) Reflection with respect to the line y=x
(ii) translation through 3 units along the positive direction of the X-axis
(iii) Rotation through an angle of π6 about the origin in the clockwise direction. The final position of the point P is
View SolutionThe point (4, 1) undergoes the following three transformations successively: (a) Reflection about the line y = x (b) Translation through a distance 2 units along the positive direction of the x-axis. (c) Rotation through an angle π4 about the origin in the anti clockwise direction. The final position of the point is given by the co-ordinates.
View SolutionThe point (4, 1) undergoes the following three transformations successively: (a) Reflection about the line y = x (b) Translation through a distance 2 units along the positive direction of the x-axis. (c) Rotation through an angle π4 about the origin in the anti clockwise direction. The final position of the point is given by the co-ordinates.
View SolutionThe point P(1,3) undergoes the following transformations successively :
(i) Reflection with respect to the line y = x
(ii) Translation through 3 units along the positive direction of the X-axis
(iii) Rotation through an angle of π6 about the origin in the clockwise direction. The final position of the point P is
View Solution
