The point at which the two coordinate axes meet is called the
abscissa
ordinate
origin
quadrant
The correct Answer is:C
The point at which the two coordinate axes meet is called the origin.
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:NCERT EXEMPLAR ENGLISHChapter:COORDINATE GEOMETRYExercise:Exercise 3.2 Very Short Answer Type Questions
Explore 1 Video
- COORDINATE GEOMETRYBook:NCERT EXEMPLAR ENGLISHChapter:COORDINATE GEOMETRYExercise:Exercise 3.3 Short Answer Type Questions
Explore 12 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Long Answer Type Questions
Explore 5 Videos
- HERON'S FORMULABook:NCERT EXEMPLAR ENGLISHChapter:HERON'S FORMULAExercise:Long Answer Type Questions
Explore 8 Videos
Similar Questions
Knowledge Check
Which point on the coordinate plane shown here is indicated by the following coordinates?
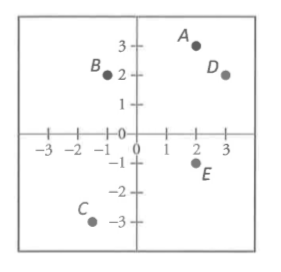 A(2,−1)B(−1.5,−3)C(−1,2)D(3,2)
A(2,−1)B(−1.5,−3)C(−1,2)D(3,2)The equation of a circle which touches both the coordinate axes and the line x = 3 is
A4x2+4y2−12x±12y+9=0B4x2+4y2+12x±12y+9=0C4x2+4y2±12x−12y+9=0D4x2+4y2±12x+12y+9=0
A line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin. If the area of the triangle OPQ is least, then the slope of the line PQ is
View SolutionA variable plane is at a distance k from the origin and meets the coordinates axes is A,B,C. Then the locus of the centroid of ΔABC is
View SolutionIf a line passes through the point (2,2) and encloses a triangle of area A square units with the coordinate axes , then the intercepts made by the line on the coordinate axes are the roots of the equations
View SolutionThe equation of the curve in which the portion of the tangent included between the coordinate axes is bisected at the point of contact, is
View SolutionIf the sum of the squares of the distance of a point from the three coordinate axes is 36, then find its distance from the origin.
View Solutiontangent drawn to the ellipse x2a2+y2b2=1 at point 'P' meets the coordinate axes at points A and B respectively.Locus of mid-point of segment AB is
View Solution