The point P is the intersection of the straight line joining the points Q(2,3,5) and R(1,−1,4) with the plane 5x−4y−z=1. If S is the foot of the perpendicular drawn from the point T(2,1,4) to QR, then the length of the line segment PS is:

A

1√2

B

√2

C

2

D

2√2

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:a

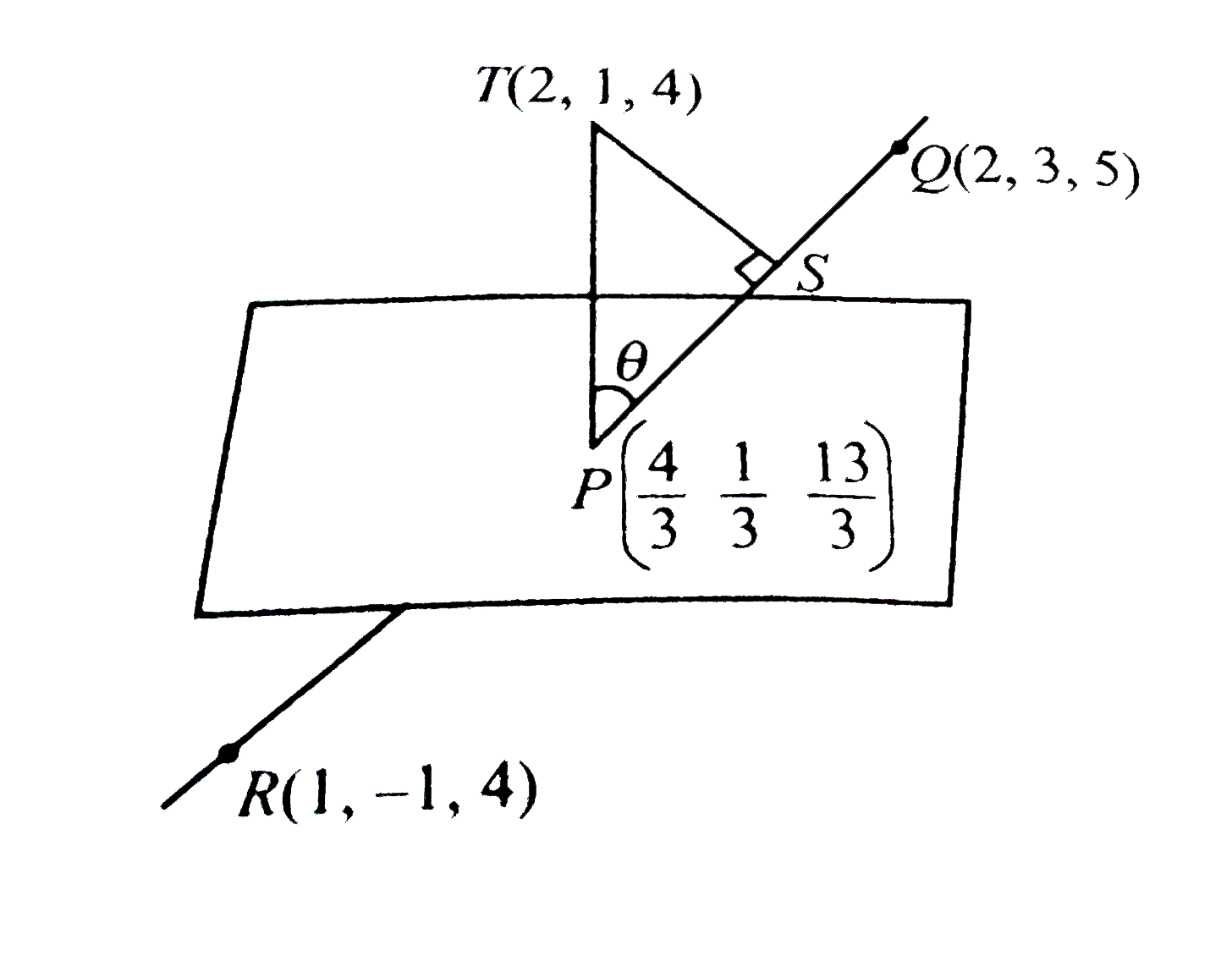
ocr_image
Direction ratios of QR are 1, 4, 1 ltBrgt Coordinate of P≡(43,13,133)
Direction ratios of PT are 2, 2, -1
Angle between QRandPT is 45∘
And PT=1
⇒ PS=TS=1√2

|
Class 12MATHSTHREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The point at which the line joining the points (2,−3,1)and(3,−4,−5) intersects the plane 2x+y+z=7 is

    A(1,2,7)
    B(1,−2,7)
    C(−1,2,7)
    D(1,−2,−7)

  • The foot of the perpendicular drawn from the point (1, 8, 4) on the line joining the points (0, -11, 4) and (2, -3, 1) is

    A(4, 5, 2)
    B(4, 5, 2)
    C(4, -5, 2)
    D(4, 5,-2)

  • The projection of the line segment joining the
    Points (1, 2, 3) and (4, 5, 6) on the plane
    2x+y+z=1 is

    A1
    B√3
    C5
    D6