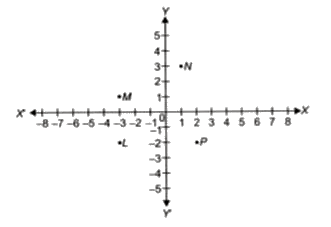
The point whose abscissa is 2 less than the ordinate is ________.
M
N
L
P
The correct Answer is:B
Step by step video, text & image solution for The point whose abscissa is 2 less than the ordinate is ________. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE GEOMETRY BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - COORDINATE GEOMETRY EXERCISE - ACHIEVERS SECTION (HOTS) (TRUE/FALSE)
1 Videos
- COORDINATE GEOMETRY BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - COORDINATE GEOMETRY EXERCISE - ACHIEVERS SECTION (HOTS)
2 Videos
- CONSTRUCTIONSBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CONSTRUCTIONSEXERCISE - Achievers Section (HOTS)
5 Videos
- HERON'S FORMULABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - HERON'S FORMULAEXERCISE - Achievers Section (HOTS)
3 Videos
Similar Questions
Knowledge Check
The point whose abscissa is equal to its ordinate and which is equidistant from A(−1,0) and B(0,5) is
A(1, 1)B(2, 2)C(-2, -2)D(3, 3)The triangle formed by the tangent to the parabola y2=4x at the point whose abscissa lies in the interval [a2,4a2], the ordinate and the X-axis, has greatest area equal to :
A12a2B8a2C16a3DNone of theseThe point (other than origin) for which abscissa is equal to the ordinate will lie in the quadrant
AI onlyBI or IICI or IIIDII or IV
Find the equations of tangent to the ellipse x216+y225=1 at a point whose abscissa is 2√2 and ordinate is positive
View SolutionFrom the given figure, answer the following questions
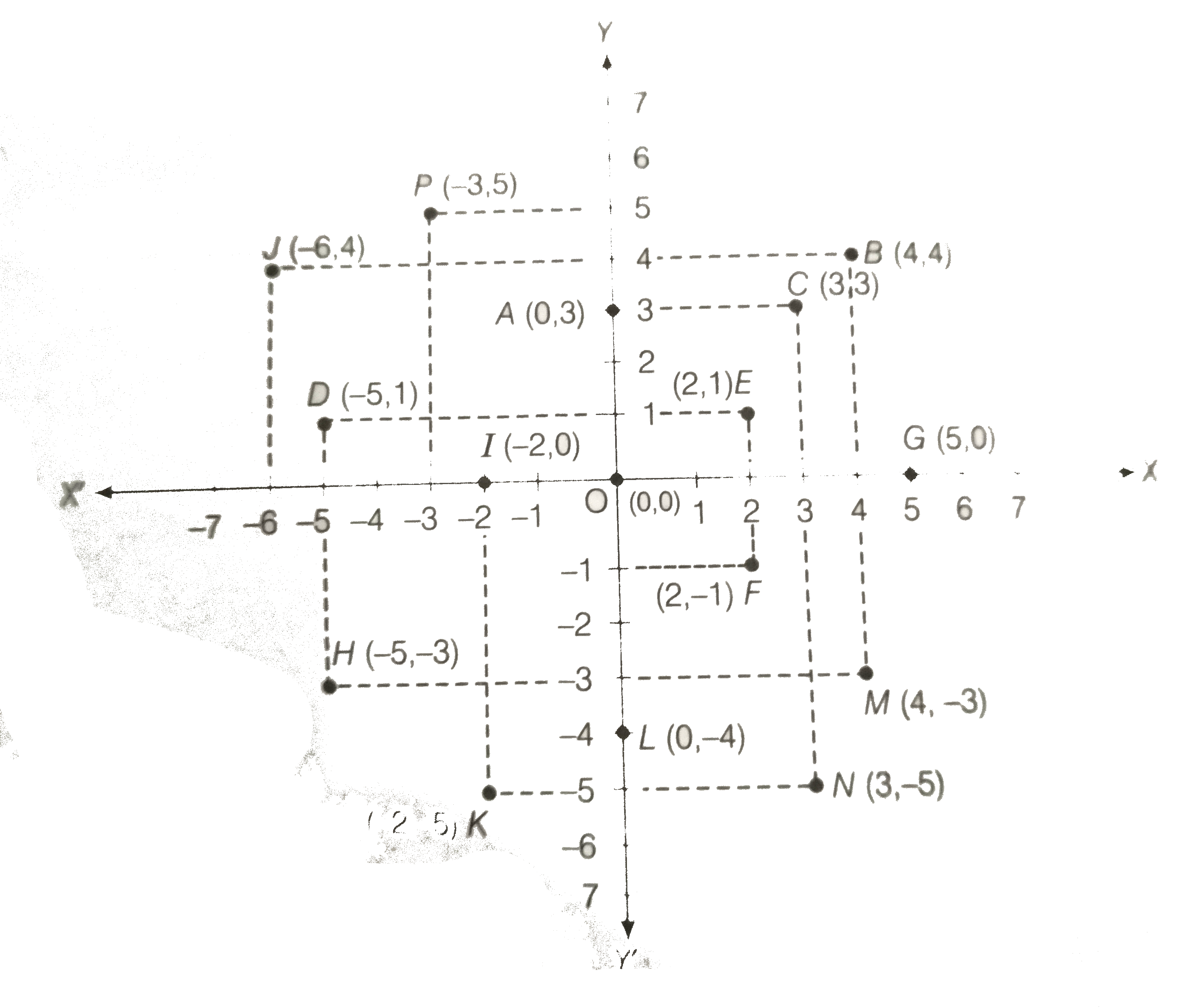
(i) Write the points whose abscissa is 0.
(ii) Write the points whose ordinate is 0.
(iii) Write the points whose abscissa is -5.
View SolutionA point whose abscissa is −3 and ordinate 2 lies in (a) First quadrant (b) Second quadrant (c) Third quadrant (d) Fourth quadrant
View SolutionThe normal chord of y2=4ax at a point where abscissa is equal to ordinate subtends at the focus an angle θ
View SolutionA particle straight line passes through orgin and a point whose abscissa is double of ordinate of the point. The equation of such straight line is :
View Solution
