The points whose abscissa and ordinate have different signs will lie in
I and II quadrants
II and III quadrants
I and III quadrants
II and IV quadrants
The correct Answer is:D
To determine in which quadrants the points whose abscissa (x-coordinate) and ordinate (y-coordinate) have different signs lie, we can analyze the signs of the coordinates in each of the four quadrants of the Cartesian plane.
1. Understanding the Quadrants:
- The Cartesian plane is divided into four quadrants:
- First Quadrant (I): Both x and y are positive. (x > 0, y > 0)
- Second Quadrant (II): x is negative, y is positive. (x < 0, y > 0)
- Third Quadrant (III): Both x and y are negative. (x < 0, y < 0)
- Fourth Quadrant (IV): x is positive, y is negative. (x > 0, y < 0)
2. Identifying Different Signs:
- We need to find the quadrants where the signs of x and y are different.
- In the Second Quadrant (II): x is negative and y is positive. (Different signs)
- In the Fourth Quadrant (IV): x is positive and y is negative. (Different signs)
3. Conclusion:
- The points whose abscissa and ordinate have different signs lie in the Second Quadrant (II) and Fourth Quadrant (IV).
Final Answer:
The points whose abscissa and ordinate have different signs will lie in the Second and Fourth Quadrants.
---
- The Cartesian plane is divided into four quadrants:
- First Quadrant (I): Both x and y are positive. (x > 0, y > 0)
- Second Quadrant (II): x is negative, y is positive. (x < 0, y > 0)
- Third Quadrant (III): Both x and y are negative. (x < 0, y < 0)
- Fourth Quadrant (IV): x is positive, y is negative. (x > 0, y < 0)
- We need to find the quadrants where the signs of x and y are different.
- In the Second Quadrant (II): x is negative and y is positive. (Different signs)
- In the Fourth Quadrant (IV): x is positive and y is negative. (Different signs)
- The points whose abscissa and ordinate have different signs lie in the Second Quadrant (II) and Fourth Quadrant (IV).
The points whose abscissa and ordinate have different signs will lie in the Second and Fourth Quadrants.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.2 Very Short Answer Type Questions1videos
COORDINATE GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.3 Short Answer Type Questions12videos
COORDINATE GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - HERON'S FORMULAEXERCISE - Long Answer Type Questions8videos
HERON'S FORMULA
Similar Questions
A point whose abscissa is −3 and ordinate 2 lies in
View SolutionA point whose abscissa and ordinate are 2 and −5 respectively, lies in
(a) First quadrant (b) Second quadrant (c) Third quadrant (d) Fourth quadrantView SolutionFrom the given figure, answer the following questions
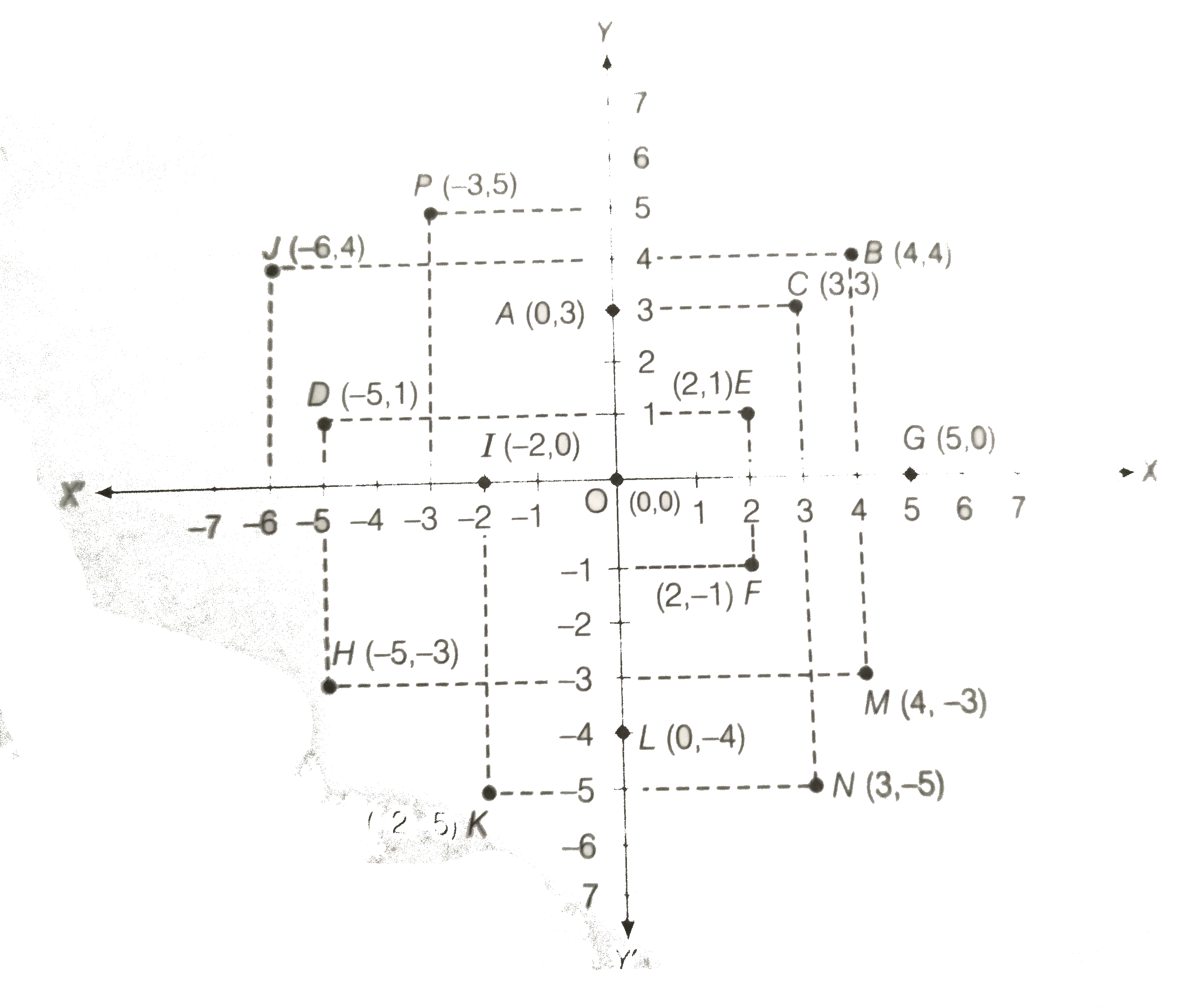
(i) Write the points whose abscissa is 0.
(ii) Write the points whose ordinate is 0.
(iii) Write the points whose abscissa is -5.View SolutionFor a given point A(0,0), ABCD is a rhombus of side 10 units where slope of AB is 43and slope of AD is 34. The sum of abscissa and ordinate of point C (where C lies in first quadrant) is
View SolutionTwo points having same abscissa but different ordinates lie on
(a) x-a xi s (b) y-a xi s (c) a line parallel to y-a xi s (d) a line parallel to x-a xi sView SolutionSigns of the abscissa and ordinate of a point in the second quadrant are respectively.
View SolutionA particle straight line passes through orgin and a point whose abscissa is double of ordinate of the point. The equation of such straight line is :
View SolutionFind a point on the curve y2=2x at which the abscissa and ordinates are increasing at the same rate.
View SolutionThe triangle formed by the tangent to the parabola y2=4x at the point whose abscissa lies in the interval [a2,4a2], the ordinate and the X-axis, has greatest area equal to :
View SolutionLet P be a point whose coordinates differ by unity and the point does not lie on any of the axes of reference. If the parabola y2=4x+1 passes through P, then the ordinate of P may be (a) 3 (b) −1 (c) 5 (d) 1
View Solution
