The population p(t) at time t of a certain mouse species satisfies the differential equation dp(t)dt=0.5p(t)−450 If p(0)=850 , then the time at which the population becomes zero is ............................................................... (1) 2 ln 18 (2) ln 9 (3) 12 In 18 (4) ln 18
2log18
log9
12log18
log18
The correct Answer is:A
Step by step video & image solution for The population p(t) at time t of a certain mouse species satisfies the differential equation d (p(t))/(dt)=0. 5 p(t)-450 If p(0)""=""850 , then the time at which the population becomes zero is ............................................................... (1) 2 ln 18 (2) ln 9 (3) 1/2 In 18 (4) ln 18 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Differential Equations Exerise 7 :
1 Videos
- DETERMINANTS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
Similar Questions
Let the population of rabbits surviving at a time t be governed by the differential equation (dptdt=12p(t)−200. If p(0)=100 , then p(t) equals
View SolutionA population p(t) of 1000 bacteria inroduced into nutrient medium grows according to the relation p(t)=1000+1000t100+t2. The maximum size of this bacterial population is
View Solution
Knowledge Check
If N= population density at time t, then population density at time t+1 can be written as. Nt+1=Nt+[(A+B)−(C+D)]. Select the correct option for A,B,C and D in the above equation.
AA can be mortality and B can be natalityBB can be immigration and C can be natalityCC can be mortality and D can be immigrationDA can be natality and D can be emigration.
Let the population of rabbits surviving at a time t be governed by the differential equation dp(t)dt=12p(t)−200. If p(0)=100 , then p(t) equals (1) 400−300et/2 (2) 300−200e−t/2 (3) 600−500et/2 (4) 40−300e−t/2
View SolutionThe set of value of 'a' which satisfy the equation ∫20(t−log2a)dt=log2(4a2) is
View SolutionA population of rabbits doubles every 48 deays according to the formula P=10(2)t48, where P is the population of rabbits on day t. what is the value of r when the population of rabbits is 320?
View SolutionIn the circuit shown in figure, circuit is closed at time t=0. At time t=ln(2) second
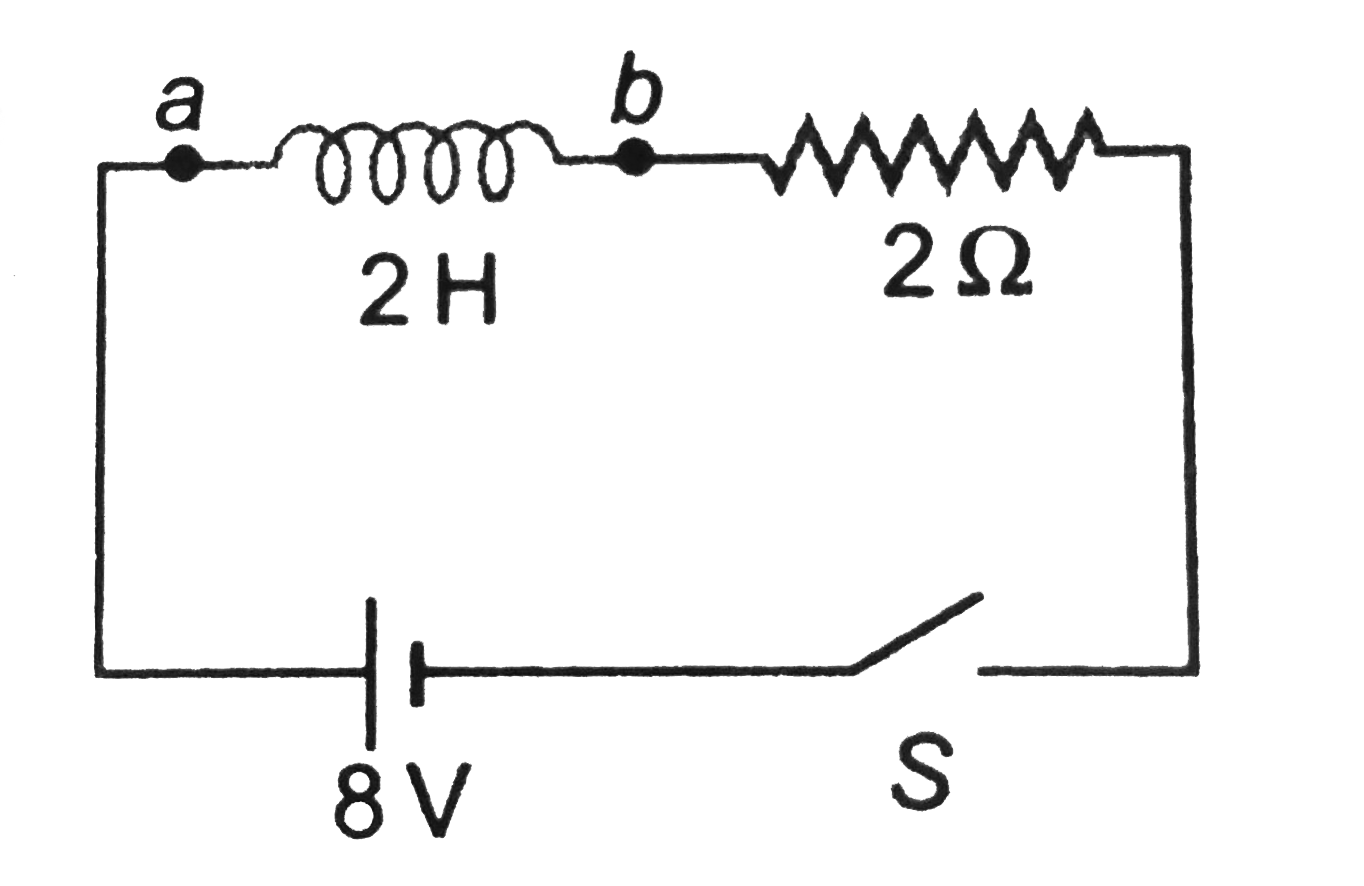
View SolutionFor a certain reaction the variation of rate constant with temperature is given by the equation
lnkt=lnk0+(ln3)t10(t≥0∘C)
The value of temperature coefficient of the reaction is
View SolutionFor a certain reaction the variation of rate constant with temperature is given by the equation
lnkt=lnk0+(ln3)t10(t≥0∘C)
The value of temperature coefficient of the reaction is
View SolutionThe dimensions of ab in the equation P=a−t2bx where P is pressure, x is distance and t is time are
View Solution
