The population p(t) at time t of a certain mouse species satisfies the differential equation dp(t)dt=0.5p(t)−450 If p(0)=850 , then the time at which the population becomes zero is ............................................................... (1) 2 ln 18 (2) ln 9 (3) 12 In 18 (4) ln 18
12ln18
ln18
2ln18
ln9
The correct Answer is:C
To solve the given differential equation for the population of the mouse species, we will follow these steps:
Step 1: Write the differential equation
The given differential equation is:
dp(t)dt=0.5p(t)−450
Step 2: Rearrange the equation
We can rearrange the equation as follows:
dp(t)dt=0.5p(t)−450
This can be rewritten as:
dp(t)dt=12p(t)−450
Step 3: Separate variables
To separate the variables, we can rewrite the equation:
dp(t)p(t)−900=12dt
Step 4: Integrate both sides
Now we integrate both sides:
∫1p(t)−900dp(t)=∫12dt
The left side integrates to:
ln|p(t)−900|=12t+C
Step 5: Solve for the constant C using the initial condition
We know that p(0)=850. Substituting t=0 and p(0)=850 into the equation gives:
ln|850−900|=12⋅0+C
This simplifies to:
ln|−50|=C⟹C=ln50
Step 6: Substitute C back into the equation
Now we substitute C back into the equation:
ln|p(t)−900|=12t+ln50
Step 7: Exponentiate both sides
Exponentiating both sides gives:
|p(t)−900|=50e12t
Since p(t)<900 for our case, we can write:
900−p(t)=50e12t
Step 8: Solve for p(t)
Rearranging gives:
p(t)=900−50e12t
Step 9: Find the time when the population becomes zero
To find the time when the population becomes zero, set p(t)=0:
0=900−50e12t
Solving for e12t:
50e12t=900⟹e12t=90050=18
Step 10: Take the natural logarithm
Taking the natural logarithm of both sides:
12t=ln18⟹t=2ln18
Conclusion
The time at which the population becomes zero is:
2ln18
The given differential equation is:
dp(t)dt=0.5p(t)−450
We can rearrange the equation as follows:
dp(t)dt=0.5p(t)−450
This can be rewritten as:
dp(t)dt=12p(t)−450
To separate the variables, we can rewrite the equation:
dp(t)p(t)−900=12dt
Now we integrate both sides:
∫1p(t)−900dp(t)=∫12dt
The left side integrates to:
ln|p(t)−900|=12t+C
We know that p(0)=850. Substituting t=0 and p(0)=850 into the equation gives:
ln|850−900|=12⋅0+C
This simplifies to:
ln|−50|=C⟹C=ln50
Now we substitute C back into the equation:
ln|p(t)−900|=12t+ln50
Exponentiating both sides gives:
|p(t)−900|=50e12t
Since p(t)<900 for our case, we can write:
900−p(t)=50e12t
Rearranging gives:
p(t)=900−50e12t
To find the time when the population becomes zero, set p(t)=0:
0=900−50e12t
Solving for e12t:
50e12t=900⟹e12t=90050=18
Taking the natural logarithm of both sides:
12t=ln18⟹t=2ln18
The time at which the population becomes zero is:
2ln18
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
6 Videos
- DIFFERENTIAL EQUATIONSBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEM)
8 Videos
- DETERMINANTSBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - DETERMINANTSEXERCISE - EXERCISE-4 : SUBJECTIVE TYPE PROBLEMS
12 Videos
- ELLIPSE BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - ELLIPSE EXERCISE - Exercise-4 : Subjective Type Problems
2 Videos
Similar Questions
Let the population of rabbits surviving at a time t be governed by the differential equation (dptdt=12p(t)−200. If p(0)=100 , then p(t) equals
View SolutionA population p(t) of 1000 bacteria inroduced into nutrient medium grows according to the relation p(t)=1000+1000t100+t2. The maximum size of this bacterial population is
View Solution
Knowledge Check
If N= population density at time t, then population density at time t+1 can be written as. Nt+1=Nt+[(A+B)−(C+D)]. Select the correct option for A,B,C and D in the above equation.
AA can be mortality and B can be natalityBB can be immigration and C can be natalityCC can be mortality and D can be immigrationDA can be natality and D can be emigration.
Let the population of rabbits surviving at a time t be governed by the differential equation dp(t)dt=12p(t)−200. If p(0)=100 , then p(t) equals (1) 400−300et/2 (2) 300−200e−t/2 (3) 600−500et/2 (4) 40−300e−t/2
View SolutionThe set of value of 'a' which satisfy the equation ∫20(t−log2a)dt=log2(4a2) is
View SolutionA population of rabbits doubles every 48 deays according to the formula P=10(2)t48, where P is the population of rabbits on day t. what is the value of r when the population of rabbits is 320?
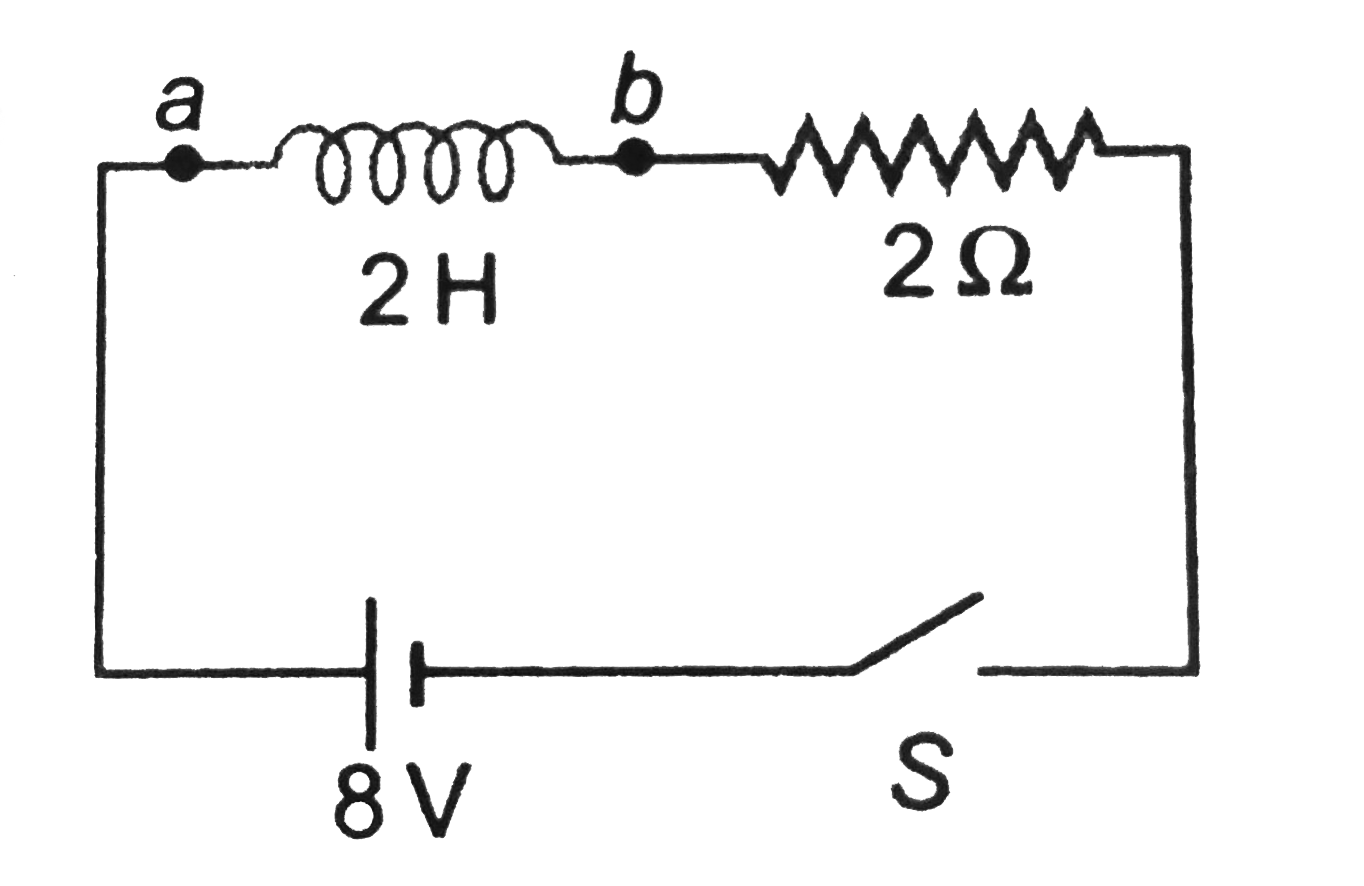
View SolutionIn the circuit shown in figure, circuit is closed at time t=0. At time t=ln(2) second
View SolutionFor a certain reaction the variation of rate constant with temperature is given by the equation
lnkt=lnk0+(ln3)t10(t≥0∘C)
The value of temperature coefficient of the reaction is
View SolutionFor a certain reaction the variation of rate constant with temperature is given by the equation
lnkt=lnk0+(ln3)t10(t≥0∘C)
The value of temperature coefficient of the reaction is
View SolutionThe dimensions of ab in the equation P=a−t2bx where P is pressure, x is distance and t is time are
View Solution
