The probability distribution of a discrate random variable X is :
X=x12345P(X=x)k2k3k4k5k
Find P(X≤4).
To find P(X≤4) for the given probability distribution of the discrete random variable X, we can follow these steps:
Step 1: Write down the probability distribution.
The probability distribution is given as:
- P(X=1)=k
- P(X=2)=2k
- P(X=3)=3k
- P(X=4)=4k
- P(X=5)=5k
Step 2: Use the property of probability distributions.
The sum of all probabilities must equal 1:
P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)=1
Substituting the probabilities:
k+2k+3k+4k+5k=1
This simplifies to:
15k=1
Step 3: Solve for k.
To find k, divide both sides by 15:
k=115
Step 4: Calculate P(X≤4).
We need to find P(X≤4), which is the sum of the probabilities for X=1,2,3, and 4:
P(X≤4)=P(X=1)+P(X=2)+P(X=3)+P(X=4)
Substituting the values:
P(X≤4)=k+2k+3k+4k
This simplifies to:
P(X≤4)=(1+2+3+4)k=10k
Now substituting k=115:
P(X≤4)=10⋅115=1015=23
Final Answer:
Thus, the probability P(X≤4) is:
23
The probability distribution is given as:
- P(X=1)=k
- P(X=2)=2k
- P(X=3)=3k
- P(X=4)=4k
- P(X=5)=5k
The sum of all probabilities must equal 1:
P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)=1
Substituting the probabilities:
k+2k+3k+4k+5k=1
This simplifies to:
15k=1
To find k, divide both sides by 15:
k=115
We need to find P(X≤4), which is the sum of the probabilities for X=1,2,3, and 4:
P(X≤4)=P(X=1)+P(X=2)+P(X=3)+P(X=4)
Substituting the values:
P(X≤4)=k+2k+3k+4k
This simplifies to:
P(X≤4)=(1+2+3+4)k=10k
Now substituting k=115:
P(X≤4)=10⋅115=1015=23
Thus, the probability P(X≤4) is:
23
Topper's Solved these Questions
- MARCH 2016BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2016EXERCISE - SECTION II
20 Videos
- MARCH 2015BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2015EXERCISE - SECTION-II
20 Videos
- MARCH 2017BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2017EXERCISE - SECTION-II
20 Videos
Similar Questions
Knowledge Check
The probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k isA1/2B5/4C3D2If the probability of a random variable X is a given below :
X=x:−2−10123P(X=x):12k152k310k
Then the value of k, is :A110B210C310D710A random variable X has following probability distribution
X=x123456P(X=x)K3K5K7K8KK
Then P(2≤X<5)= . . . .A35B725C2325D2425
If the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability distribution of X is as follows:
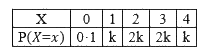
Find k and P [X<2].
View SolutionThe probability distribution of a random variable X is given as under: P(X=x)={kx2forx=1,2,32kxforx=4,5,60otherwise , where k is a constant. Find (i) P(X≥4 ) (ii) E(X) (iii) E(3X2)
View SolutionThe probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View SolutionThe probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
View Solution
