The radii of two concentric circles are 4 cm and 5 cm. The difference in the areas of these two circles is :
π
7π
9π
13π
The correct Answer is:C
To find the difference in the areas of two concentric circles with radii of 4 cm and 5 cm, we can follow these steps:
Step 1: Identify the radii of the circles.
- The radius of the first circle (C1) is 5 cm.
- The radius of the second circle (C2) is 4 cm.
Step 2: Use the formula for the area of a circle.
The area A of a circle is given by the formula:
A=πr2
where r is the radius of the circle.
Step 3: Calculate the area of the larger circle (C1).
Using the radius of the first circle (5 cm):
AC1=π(5)2=π×25=25πcm2
Step 4: Calculate the area of the smaller circle (C2).
Using the radius of the second circle (4 cm):
AC2=π(4)2=π×16=16πcm2
Step 5: Find the difference in the areas.
To find the difference in the areas of the two circles, subtract the area of the smaller circle from the area of the larger circle:
Difference=AC1−AC2=25π−16π=(25−16)π=9πcm2
Final Answer:
The difference in the areas of the two circles is 9πcm2.
---
- The radius of the first circle (C1) is 5 cm.
- The radius of the second circle (C2) is 4 cm.
The area A of a circle is given by the formula:
A=πr2
where r is the radius of the circle.
Using the radius of the first circle (5 cm):
AC1=π(5)2=π×25=25πcm2
Using the radius of the second circle (4 cm):
AC2=π(4)2=π×16=16πcm2
To find the difference in the areas of the two circles, subtract the area of the smaller circle from the area of the larger circle:
Difference=AC1−AC2=25π−16π=(25−16)π=9πcm2
The difference in the areas of the two circles is 9πcm2.
Topper's Solved these Questions
- AREAS RELATED TO CIRCLES BOOK - EDUCART PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLES EXERCISE - OBJECTIVE TYPE QUESTION (FILL IN THE BLANKS)
8 Videos
- AREAS RELATED TO CIRCLES BOOK - EDUCART PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLES EXERCISE - OBJECTIVE TYPE QUESTION (VERY SHORT QUESTIONS)
12 Videos
- ARITHMETIC PROGRESSIONSBOOK - EDUCART PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - LONG ANSWER TYPE QUESTIONS
44 Videos
Similar Questions
If the radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
View SolutionIf radii of two concentric circles are 12 cm and 13 cm, find the length of each chord of one circle which is tangent to the other circle.
View Solution
Knowledge Check
If radii of two concentric circles are 4 cm and 5 cm Then the length of the chord of one circle which is tangent to the other circle is
A3 cmB6 cmC9 cmD1 cmThe radii of two concentric circles are 19 cm and 16 cm respectively. The area of the ring enclosed by these circles is
A320cm2B330cm2C332cm2D340cm2If radii of two concentric circles are 4 cm and 5 cm, then length of each chord of one circle which is tangent to the other circle, is
A3 cmB6 cmC9 cmD1 cm
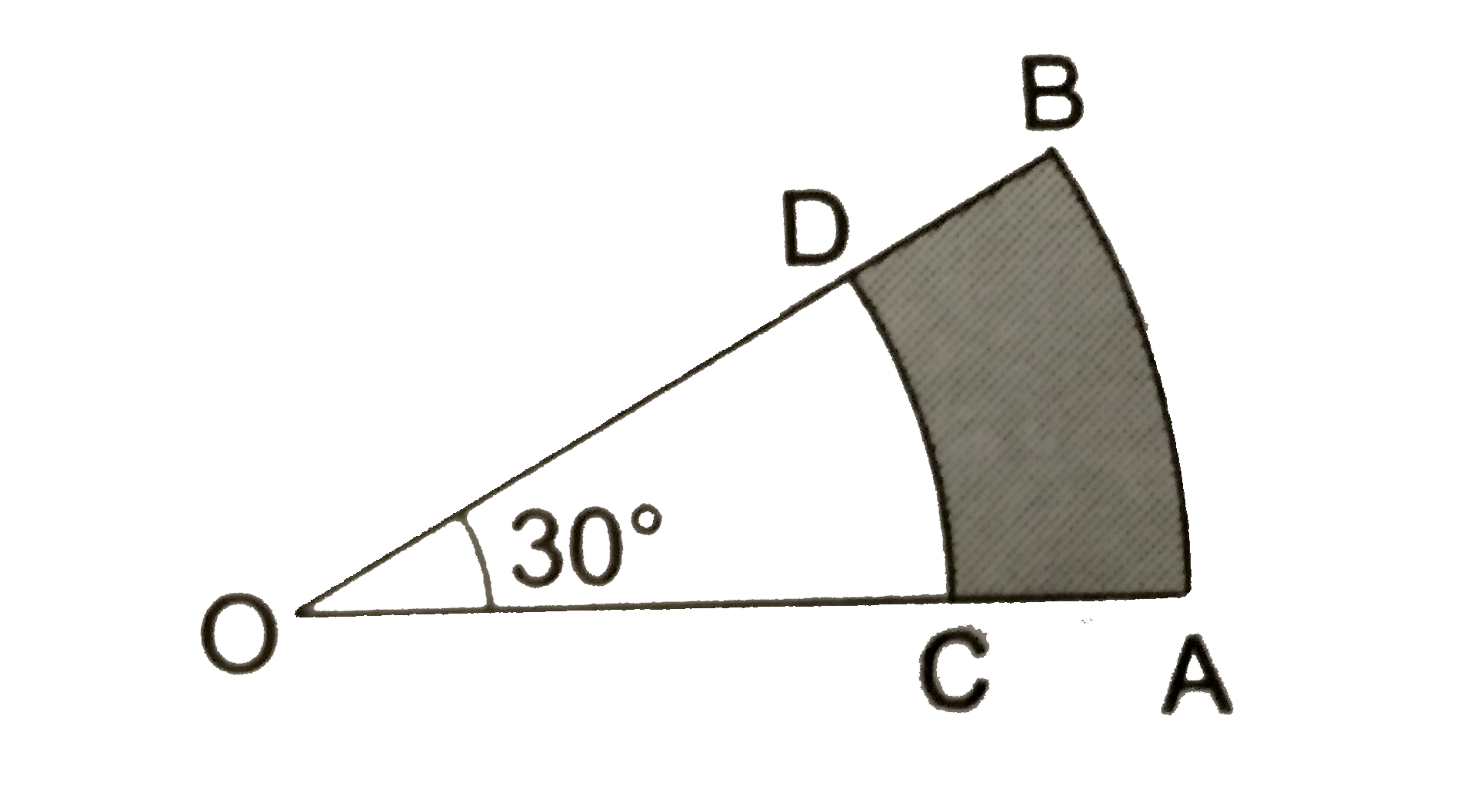
In the give figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
View SolutionThe radius of the two concentric circles is 5 cm and 13 cm. The tangent to the smaller circle is the chord to the greater circle. What is the length (in cm) of that chord?
View SolutionThe radius of the two concentric circles is 5 cm and 13 cm. The tangent to the smaller circle is the chord to the greater circle. What is the length (in cm) of that chord?
View SolutionThe difference between the radii of the smaller circle and the bigger circle is 7 cm and the difference between the areas of the two circles is 1078 sq cm. What is the radius of the smaller circle in cm?
View SolutionThe areas of two concentric circles are 1386cm2 and 962.5cm2.The width of the ring is
View Solution
