The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length is
cm
cm
cm
cm
The correct Answer is:B
To solve the problem, we will follow these steps:
1. Understand the given information: We have a circle with a radius of 6 cm, and there is a chord of length 8 cm. We need to find the perpendicular distance from the center of the circle to the chord.
2. Draw the diagram:
- Draw a circle with center O.
- Draw a chord AB of length 8 cm.
- Draw a perpendicular line from the center O to the chord AB, meeting the chord at point M.
3. Identify the segments:
- Since OM is perpendicular to AB, it bisects the chord. Therefore, AM = MB = 8 cm / 2 = 4 cm.
4. Apply the Pythagorean theorem:
- In triangle OMA, we can apply the Pythagorean theorem.
- Here, OA is the radius (6 cm), AM is half the chord length (4 cm), and OM is the perpendicular distance we want to find (let's denote it as h).
According to the Pythagorean theorem:
OA2=OM2+AM2
Substituting the known values:
62=h2+42
5. Calculate the squares:
- 62=36
- 42=16
So, we have:
36=h2+16
6. Rearrange the equation:
h2=36−16
h2=20
7. Find h:
h=√20=√4×5=2√5
8. Conclusion: The perpendicular distance from the center of the circle to the chord is 2√5 cm.
- Draw a circle with center O.
- Draw a chord AB of length 8 cm.
- Draw a perpendicular line from the center O to the chord AB, meeting the chord at point M.
- Since OM is perpendicular to AB, it bisects the chord. Therefore, AM = MB = 8 cm / 2 = 4 cm.
- In triangle OMA, we can apply the Pythagorean theorem.
- Here, OA is the radius (6 cm), AM is half the chord length (4 cm), and OM is the perpendicular distance we want to find (let's denote it as h).
OA2=OM2+AM2
62=h2+42
- 62=36
- 42=16
36=h2+16
h2=36−16
h2=20
h=√20=√4×5=2√5
Topper's Solved these Questions
- CIRCLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - QUESTION BANK - 28
1 Videos
- CIRCLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - QUESTION BANK - 29
1 Videos
- CIRCLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - QUESTION BANK - 26
1 Videos
- AVERAGEBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGEEXERCISE - SELF ASSESSMENT SHEET
10 Videos
- CO-ORDINATE GEOMETRYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Self Assessment Sheet
10 Videos
Similar Questions
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is √5 cm (b) 2√5 cm (c) 2 √7 cm (d) √7 cm
Let AB be chord, OL is the perpendicular distance.
In right △OAL,OA2=AL2+OL2
(6)2=(82)2+OL2
AL=12AB
36=16+OL2
OL2=36−16=20
OL=√20=√4×5=2√5cm
View SolutionThe radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
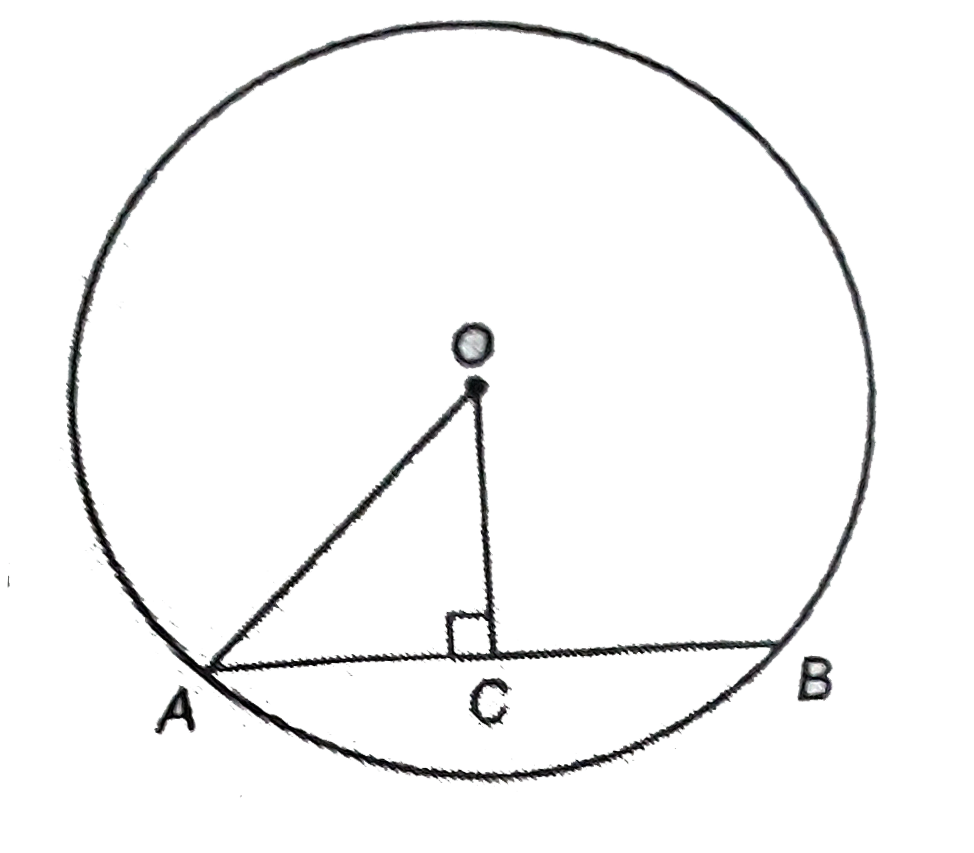
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
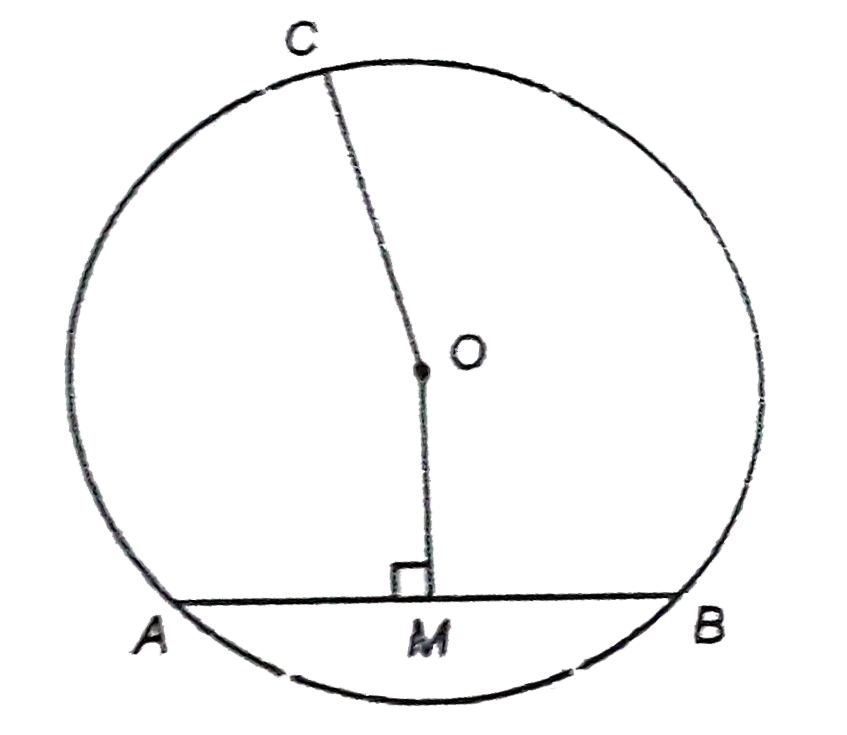
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
View Solution
Knowledge Check
The length of the chord of a circle is 8 cm and perpendicular distance between centre and the chord is 3 cm. Then the radius of the circle is equal to :
A4 cmB5 cmC6 cmD8 cmThe radius of a circle is 13 cm and XY is a chord which is at a distance of 12 cm from the centre. The length of the chord is:
A15 cmB12 cmC10 cmD20 cm
Radius of circle is 34 cm. And distance of chord from centre is 24 cm. Find length of the chord?
View SolutionIf the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is 15 cm (b) 16 cm (c) 17 cm (d) 34 cm
View SolutionThe radius of a circle is 5 cm and the distance of a chord from the centre is 3 cm . Find the length of the chord.
View SolutionPS is the chord of the circle with centre O. A perpendicular is drawn from centre O of the circle to chord PS at M. If ¯¯¯¯¯PS=30cm and ¯¯¯¯¯¯¯OM=8cm, then find the radius of the circle.
View SolutionRadius of a circle is 34 cm and the distance of the chord from the centre is 30 cm, find the length of the chord .
View SolutionPS is the chord of the circle with centre O. A perpendicular is drawn from centre O of the circle to chord PS at M. If ¯¯¯¯¯PS=30cm and ¯¯¯¯¯¯¯OM=8cm, then find the radius of the circle.
View Solution
