The radius of a circle is 8 cm and O is its centre. If and AB is a chord, then what is the length of the chord AB?
The correct Answer is:8 cm
To find the length of the chord AB in a circle with radius 8 cm and a central angle AOB of 60 degrees, we can follow these steps:
1. Identify the Given Information:
- Radius of the circle (OA and OB) = 8 cm
- Angle AOB = 60 degrees
2. Understanding the Triangle:
- Triangle AOB is formed by the two radii OA and OB and the chord AB.
- Since OA and OB are both radii of the circle, they are equal in length.
3. Using the Properties of Triangles:
- In triangle AOB, we know that the sum of the angles in a triangle is 180 degrees.
- Therefore, we can set up the equation for the angles:
∠AOB+∠OAB+∠OBA=180∘
- Let the angles OAB and OBA be equal (let's call them x). Thus, we have:
60∘+x+x=180∘
- Simplifying this gives:
60∘+2x=180∘
2x=180∘−60∘=120∘
x=60∘
4. Conclusion about the Triangle:
- Since all angles in triangle AOB are 60 degrees, triangle AOB is an equilateral triangle.
5. Finding the Length of the Chord AB:
- In an equilateral triangle, all sides are equal. Therefore:
AB=OA=OB
- Since OA and OB are both radii of the circle, we have:
AB=8 cm
Final Answer:
The length of the chord AB is 8 cm.
---
- Radius of the circle (OA and OB) = 8 cm
- Angle AOB = 60 degrees
- Triangle AOB is formed by the two radii OA and OB and the chord AB.
- Since OA and OB are both radii of the circle, they are equal in length.
- In triangle AOB, we know that the sum of the angles in a triangle is 180 degrees.
- Therefore, we can set up the equation for the angles:
∠AOB+∠OAB+∠OBA=180∘
- Let the angles OAB and OBA be equal (let's call them x). Thus, we have:
60∘+x+x=180∘
- Simplifying this gives:
60∘+2x=180∘
2x=180∘−60∘=120∘
x=60∘
- Since all angles in triangle AOB are 60 degrees, triangle AOB is an equilateral triangle.
- In an equilateral triangle, all sides are equal. Therefore:
AB=OA=OB
- Since OA and OB are both radii of the circle, we have:
AB=8 cm
The length of the chord AB is 8 cm.
Topper's Solved these Questions
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Short Answer Type Questions
19 Videos
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Essay Type Questions
5 Videos
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Level 3
21 Videos
- MATRICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MATRICESEXERCISE - EXERCISE CONCEPT APPLICATION (LEVEL 3)
15 Videos
- MODULAR ARITHMETIC BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MODULAR ARITHMETIC EXERCISE - Level 3
15 Videos
Similar Questions
The radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
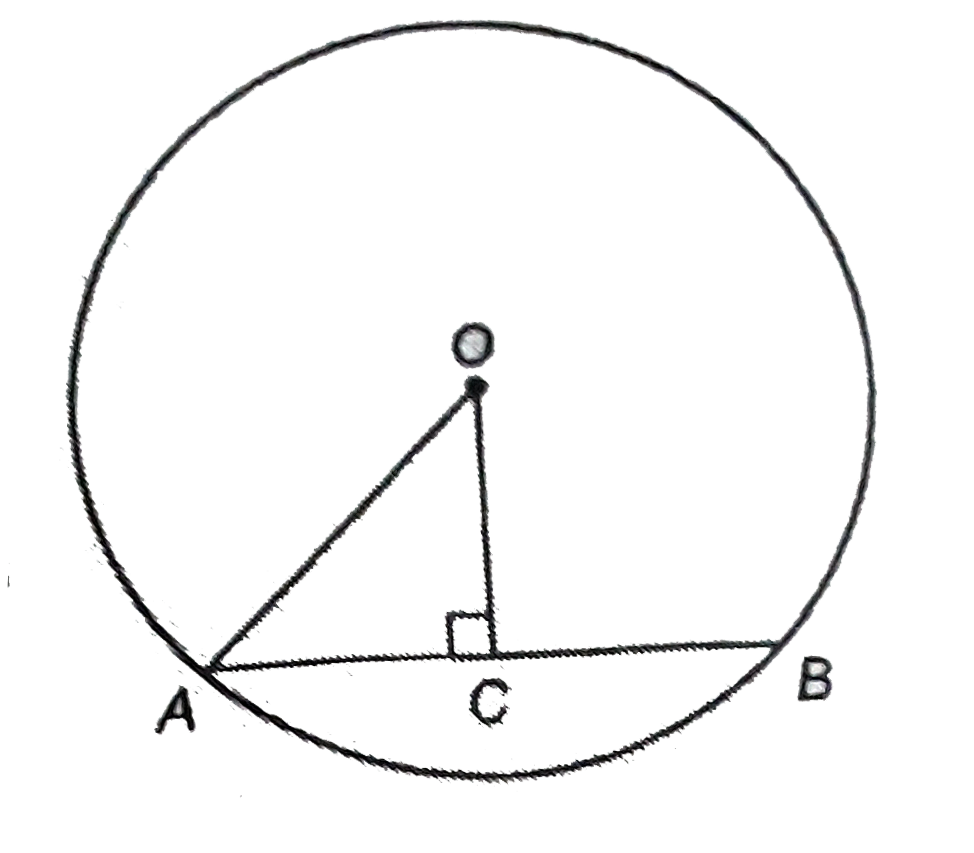
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
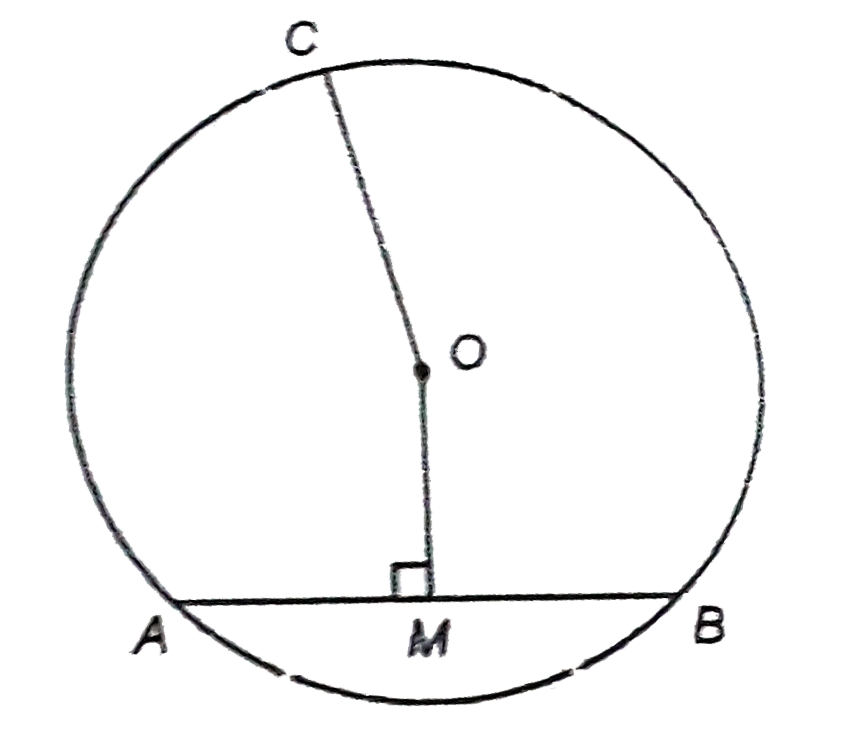
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
View SolutionThe radius of a circle is 5 cm and the length of one of its chords is 6 cm, the distance of the chord from the centre will be
View Solution
Knowledge Check
The radius of a circle is 13 cm and the length of one of its chords is 10 cm . The distance of the chord from the centre is
A12 cmB9 cmC10 cmD15 cmIn the given figure, O is the centre of a circle of radius 13 cm and AB is a chord perpendicular to OD. If CD = 8 cm, then what is the length (in cm) of AB?
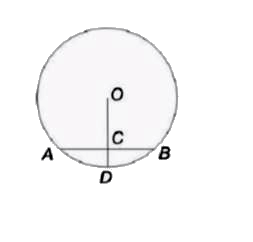 AA)6 cmBB)12 cmCC)24 cmDD)28cm
AA)6 cmBB)12 cmCC)24 cmDD)28cmThe length of the radius of a circle with centre O is 5 cm and the length of the chord AB is 8 cm. The distance of the chord AB from the point O is
A2 cm.B3 cm.C4 cm.D15 cm.
In a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC
View SolutionThe radius of a circle is 8cm and the length of one of its chords is 12cm. Find the distance of the chord from the centre.
View SolutionIn a circle of radius 5 cm, AB and Ac are two chords of 6cm each. Find the length of the chord BC.
View SolutionIn a circle of radius 17 cm a chord is at a distance of 15 cm form the centre of the circle. What is the length of the chord ?
View SolutionThe radius of a circles is 13cm and the length of one of its chords is 10cm. Find the distance of the chord from the centre.
View Solution
