The radius of the circle passing through the foci of the ellipse x216+y29 and having its center (0, 3) is 4 (b) 3 (c) √12 (d) 72Solution in Bengali
x2+y2−6y−7=0
x2+y2−6y+7=0
x2+y2−6y−5=0
x2+y2−6y+5=0
Coordinates for focia re (ae, 0) , (-ar, 0)
∴e=√1−916⇒e=√74
Coordinates of foci are (√7,0),(−√7,0)
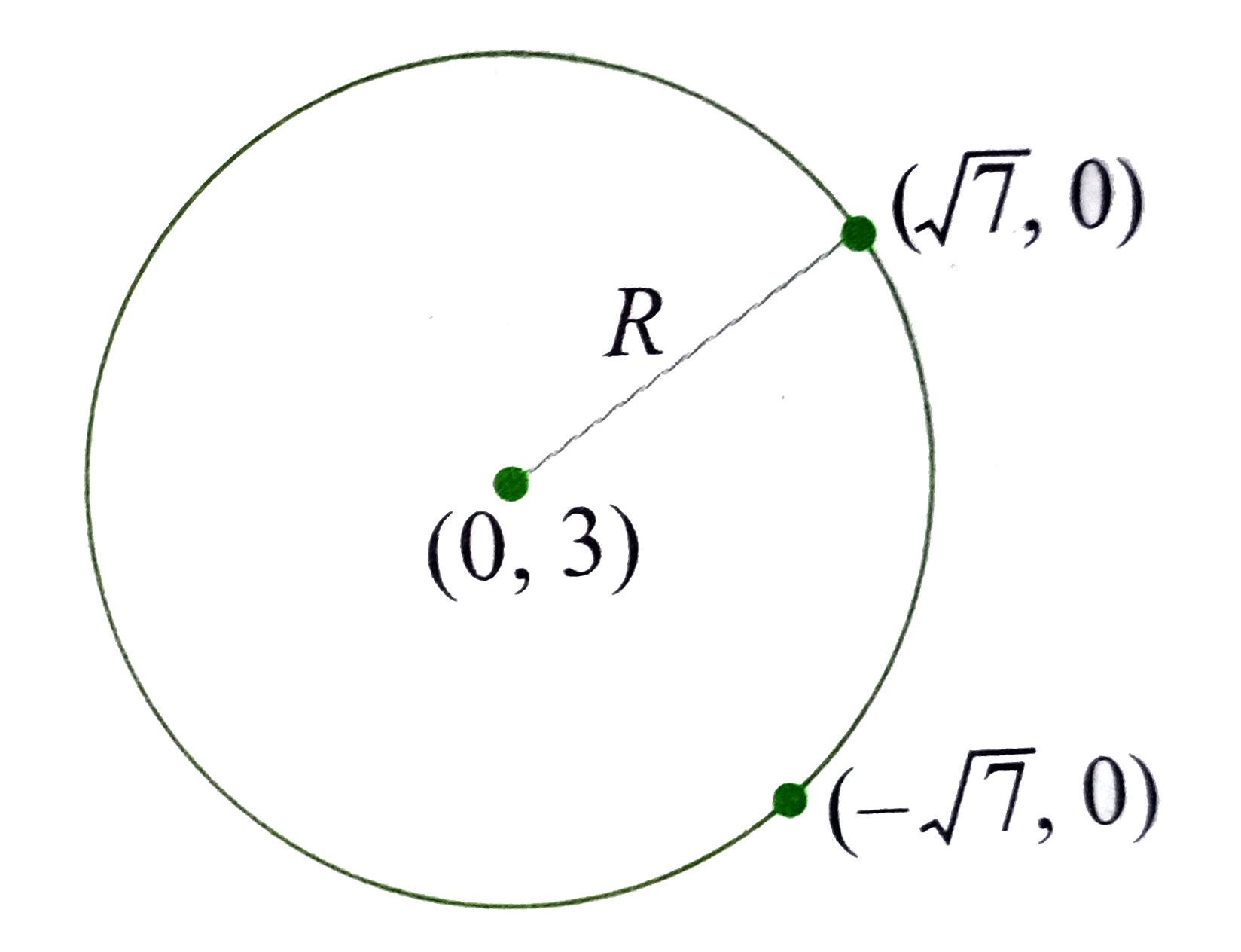
Radius R=√7+9=4
Thus, equation of circle is (x−0)2+(y−3)2=42orx2+y2−6y+9=16
or x2+y2−6y7=0
Similar Questions
The equation of the circle passing through the foci of the ellipse (x^(2))/(16)+(y^(2))/(9)=1 , and having centre (0, 3) is :
View SolutionThe radius of the circle passing through the foci of the ellipse (x^(2))/(16)+(y^(2))/(9)=1 , and having its centre (0, 3) is :
View SolutionThe radius of the circle passing through the foci of the ellipse (x^2)/(16)+(y^2)/9 and having its center (0, 3) is 4 (b) 3 (c) sqrt(12) (d) 7/2
View SolutionThe equation of the circle passing through the foci of the ellipse (x^(2))/(16) + (y^(2)) /(9) = 1 and having centre at (0 , 3) is _
View Solutionthe radius of the circle passing through the foci of the ellipse (x^(2))/(16)+(y^(2))/(9)=1 and having centre at (0,3) is
View SolutionThe radius of the circle passing through the foci of the ellipse (x^(2))/(16) + (y^(2))/( 9) = 1 and having its centre at (0,3) is
View SolutionThe radius of the circle passing through the foci of the ellipse (x^2)/(16)+(y^2)/9 and having its center (0, 3) is (a)4 (b) 3 (c) sqrt(12) (d) 7/2
View SolutionThe radius of the circle passing through the foci of the ellipse x^2/16+y^2/9=1 and having centre at (0,3) is :
View Solution
