The radius of the circle passing through the vertices of the triangle formed by the lines x+y=2,3x−4y=6,x−y=0
Video Solution
Text Solution
Let the sides AB, BC and CA of ΔABC be represented by the equations x+y=2,3x−4y=6andx−y=0 respectively.
Solving x+y=2and3x−4y=6, we get B(2,0).
Solving 3x−4y=6andx−y=0, we get C(−6,−6).
Solving x+y=2andx−y=0, we get A(1,1)
Let the required equation of the circle be
x2+y2+2gx+2fy+c=0 ... (i)
Since it passes through A(1,1),B(2,0)andC(−6,−6), each of these points must satisfy (i)
∴12+12+2g+2f+c=0⇒2g+2f+c+2=0 ... (ii)
22+02+4g+c=0⇒4g+c+4=0 ... (iii)
(−6)2+(−6)2−12g−12f+c=0⇒−12g−12f+c+72=0 ... (iv)
Substracting (ii) from (iii), we get
2g−2f+2=0⇔g−f=−1 ...(v)
Substracting (iv) from (iii), we get
16g+12f−68=0⇔4g+3f=17 ... (vi)
Solving (v) and (vi), we get g=2andf=3
Putting g=2 in (iii), we get c=−12
Hence, the required equation is
x2+y2+4x+6y−12=0
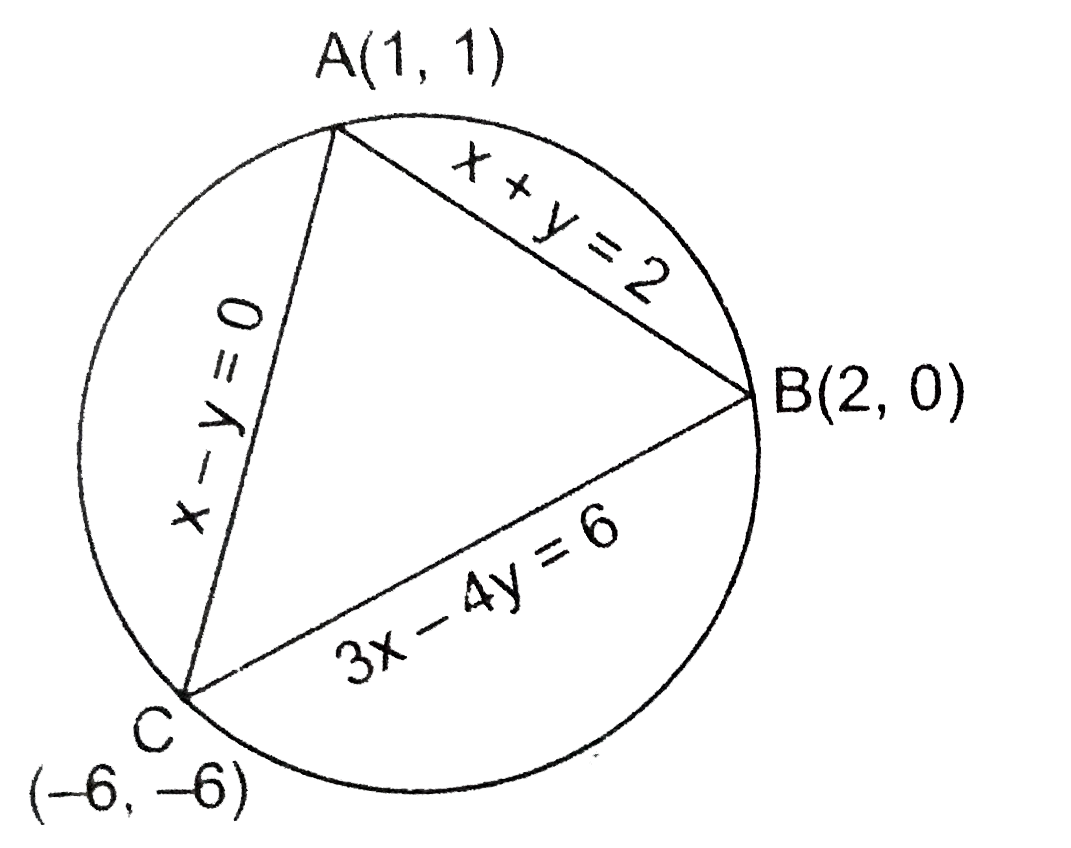
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 A14videos
CIRCLE
- BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 B18videos
CIRCLE
- BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B16videos
BINOMIAL THEOREM
- BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Exercise 9D18videos
COMBINATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The incentre of triangle formed by lines x=0,y=0 and 3x+4y=12 is
A(3,1)B(1,2)C(2,1)D(1,1) - Question 2 - Select One
Area of triangle formed by straight lines 3x−y=3,x−2y+4=0andy=0 is
A154 sq. unitB152 sq. unitC15 sq. unitDCannot be determined
Find the equation of the circle passing through the vertices of the triangle whose sides are :
x - y = 0 , 3x + 2y = 5 and x + 2y = 5 .View SolutionThe triangle formed by the lines x+y=0,3x+y=4,x+3y=4 is
View SolutionFind the orthocenter of the triangle formed by the lines x+2y=0,4x+3y−5=0,3x+y=0.
View SolutionDetermine the vertices of the triangle formed by the lines 4x−y=4, 4x+y=12 and the x - axis.
View SolutionDetermine graphically, the vertices of the triangle formed by the lines
y=x, 3y=x and x+y=8View SolutionThe orthocenter of the triangle formed by the lines x+y+1=0,x−y−1=0,3x+4y+5=0 is :
View Solution

