The rate of change of radius of a circle is 1 cm / sec. Match the following

A

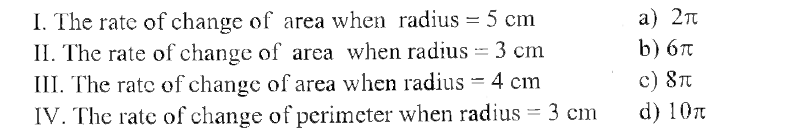
d,b,c,a

B

d,c,b,a

C

c,d,b,a

D

a,d,b,c

Text Solution

Verified by Experts

The correct Answer is:A

|

Class 12 MATHS CONTINUITY AND DIFFERENTIABILITY

Topper's Solved these Questions

APPLICATIONS OF DIFFERENTIATIONBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - APPLICATIONS OF DIFFERENTIATIONEXERCISE - EXERCISE 2 SET-4 (SPECIAL TYPE QUESTIONS)
15 Videos
APPLICATIONS OF DIFFERENTIATIONBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - APPLICATIONS OF DIFFERENTIATIONEXERCISE - EXERCISE 2 SET-2 (SPECIAL TYPE QUESTIONS)
11 Videos
ADDITION OF VECTORS BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - ADDITION OF VECTORS EXERCISE - EXERCISE 2 SET - 4
8 Videos
BINOMIAL THEOREMBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 4
4 Videos

Similar Questions

Knowledge Check

If the rate of increase of the radius of a circle is 5 cm/sec, then the rate of increase of its area, when the radius is 20 cm, will be
A $10 π$
B $20 π$
C $200 π$
D $400 π$
The rate of change of the area of a circle with respect to its radius at r = 2 cm is :
A $8 π$
B $2 π$
C $4 π$
D $11 π$
If the rate of change in the circumference of a circle of 0.3 cm/s then the rate of change in the area of the circle when the radius is 5 cm, is
A1.5 sq cm/s
B0.5 sq cm/s
C5 sq cm/s
D3 sq cm/s

DIPTI PUBLICATION ( AP EAMET)-APPLICATIONS OF DIFFERENTIATION-EXERCISE 2 SET-3 (SPECIAL TYPE QUESTIONS)

Home
Ask Doubt
Profile