The ratio of the curved surfaces areas of a solid right circular cone and of a right circular cylinder both of same radius of base and of same height is 5 : 8 . Then find the ratio of their radius of base and height . Solution in Bengali
Let radius of base = r unit
and height of them = h unit
Also, let the slant height of the cone = l unit
∴ curved surface of the cone = πrl wq- unit
=πr√r2+h2sq - unit
The curved surface area of the cylinder = 2πrh sq - unit
As per question , pr√π2+h22prh=58
or , √r2+h2h=54or,r2+h2h2=2516or,r2h2+1=2516
or,r2h2=2516−1or,r2h2=916or,rh=√916=34
⇒r:h=3:4
⇒r:h=3:4
Hence the required ratio of the radius of base and the height = 3:4
Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - PROBLEMS RELATED TO DIFFERENT SOLIDS AND OBJECTS EXERCISE - Exercise -5 (Multiple choice question )5videos
PROBLEMS RELATED TO DIFFERENT SOLIDS AND OBJECTS
- BOOK - CALCUTTA BOOK HOUSECHAPTER - PROBLEMS RELATED TO DIFFERENT SOLIDS AND OBJECTS EXERCISE - Write true or false2videos
PROBLEMS RELATED TO DIFFERENT SOLIDS AND OBJECTS
- BOOK - CALCUTTA BOOK HOUSECHAPTER - PARTNERSHIP BUSINESSEXERCISE - LONG ANSWER TYPE QUESTIONS17videos
PARTNERSHIP BUSINESS
- BOOK - CALCUTTA BOOK HOUSECHAPTER - PYTHAGORAS THEOREM EXERCISE - EXAMPLE 64videos
PYTHAGORAS THEOREM
Similar Questions
If a sphere is made by melting a solid right circular cylinder of radus 2x cm and height x cm , then the radius of the sphere will be
02:35View SolutionA right circular cone of radius x cm and of height h cm is placed on a hemisphere . Then the total surface area of the newly constructed solid object will be πr(√h2+r2+2r) sq- cm
00:45View SolutionAshim, Rana and Bapi started a business with captials Rs. 1500, Rs. 1000 and Rs. 1750 respectively. If the total loss at the end of the uear be Rs. 425, then find th loss of each of them.
01:03View SolutionA person at first travels 28m east from a certain place and then he travels √57m south of it. The distance of the person from the starting point will be
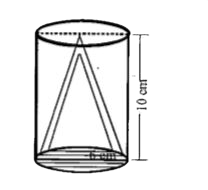
03:25View SolutionFrom a right circular cylinder with height 10cm and radius of base 6cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
04:27View SolutionThe ratio of the volumes of a right circular cylinder and a right circular cone of the same base and the same height will be
03:20View SolutionA right circular cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is
02:45View SolutionThe curved surface area of a right circular cone is √5 times of its base area . Find the ratio of the height and the length of radius of the cone.
02:56View SolutionThe radius of base and height of a right circular cone are equal . If the cone be melted to make a right circular cylinder of same radius , then what will be the ratio of the height of cylinder and the slant height of the cone ?
02:18View SolutionThe radius and height of the base of an elliptical cylinder and an elliptical cone are the same. If the ratio of the areas of their back surface is 8: 5, then find the ratio of their base radius and height.
05:34View SolutionFrom a right circular cylinder with height 10cm and radius of base 6cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
View SolutionFrom a right circular cylinder with height 10cm and radius of base 6cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
02:36View SolutionFrom a right circular cylinder with height 10cm and radius of base 6cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
02:19View Solutionएक लंब वृत्तीय बेलन और एक लंब वृत्तीय शंकु बराबर आधार ऊँचाई के है। यदि उनके वक्र पृष्ठ 8 : 5 के अनुपात में हों, तो उनमें से किसी एक के आधार की त्रिज्या और ऊँचाई का अनुपात ज्ञात कीजिए।
01:56View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the the same height and same base is removed . find the volume of the remaining solid
 01:03View Solution
01:03View Solution

