The remainder when 9103 is divided by 25 is equal to
A
5
B
6
C
4
D
none of these
Video Solution
Text Solution
The correct Answer is:c
We have,
9103
=9×(81)51
= 9(80+1)51
=9{51C0(80)51+51C1(80)50+51C2(80)49+...+51C50(80)+1}
9[25k+(51×80+1)]
=25kλ+36729
25λ+25×1469+4
25(λ+1469)+4 Hence, the remainder is 4,
|
Topper's Solved these Questions
- BINOMIAL THEOREM AND ITS APPLCIATIONS Book:OBJECTIVE RD SHARMAChapter:BINOMIAL THEOREM AND ITS APPLCIATIONS Exercise:Section I - Assertion Reason Type
Explore 13 Videos
- BINOMIAL THEOREM AND ITS APPLCIATIONS Book:OBJECTIVE RD SHARMAChapter:BINOMIAL THEOREM AND ITS APPLCIATIONS Exercise:Exercise
Explore 107 Videos
- BINOMIAL THEOREM AND ITS APPLCIATIONS Book:OBJECTIVE RD SHARMAChapter:BINOMIAL THEOREM AND ITS APPLCIATIONS Exercise:Chapter Test
Explore 60 Videos
- CARTESIAN CO-ORDINATE SYSTEM Book:OBJECTIVE RD SHARMAChapter:CARTESIAN CO-ORDINATE SYSTEM Exercise:Exercise
Explore 29 Videos
Similar Questions
Knowledge Check
The remainder when 9+6 is divided by 8 is
A2B3C5D7The remainder when ('(2)^(54)' -1) is divided by 9 is :
AA)0BB)8CC)7DD)none of theseThe remainder when 6n−5n is divided by 25, is
A1B2C3D7
The remainder when 487+687 is divided by 25, is
View SolutionUsing Binomial theorem, find the remainder when 5103 is divided by 13.
View SolutionThe remainder when 6n−5n is divided by 25, is
View SolutionThe remainder when
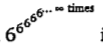 is divided by 10 is :
is divided by 10 is :
View SolutionThe remainder when (254−1) is divided by 9 is :
View Solution
