The scores of a batsman in ten innings are : 38,70,48,34,42,55,63,46,54,44. Find the mean deviation about the median.
To find the mean deviation about the median for the given scores of a batsman in ten innings, we will follow these steps:
Step 1: List the Scores
The scores of the batsman in ten innings are:
38, 70, 48, 34, 42, 55, 63, 46, 54, 44.
Step 2: Arrange the Scores in Ascending Order
We need to arrange these scores in ascending order:
34, 38, 42, 44, 46, 48, 54, 55, 63, 70.
Step 3: Find the Median
Since there are 10 scores (even number), the median is the average of the 5th and 6th terms in the ordered list.
- The 5th term is 46.
- The 6th term is 48.
Now, calculate the median:
Median=46+482=942=47.
Step 4: Calculate the Deviations from the Median
Next, we calculate the absolute deviations of each score from the median (47):
- |34 - 47| = 13
- |38 - 47| = 9
- |42 - 47| = 5
- |44 - 47| = 3
- |46 - 47| = 1
- |48 - 47| = 1
- |54 - 47| = 7
- |55 - 47| = 8
- |63 - 47| = 16
- |70 - 47| = 23
Step 5: Sum of Absolute Deviations
Now, sum all the absolute deviations:
13+9+5+3+1+1+7+8+16+23=86.
Step 6: Calculate the Mean Deviation
Finally, we calculate the mean deviation by dividing the sum of absolute deviations by the number of scores (10):
Mean Deviation=8610=8.6.
Final Answer
The mean deviation about the median is 8.6.
---
The scores of the batsman in ten innings are:
38, 70, 48, 34, 42, 55, 63, 46, 54, 44.
We need to arrange these scores in ascending order:
34, 38, 42, 44, 46, 48, 54, 55, 63, 70.
Since there are 10 scores (even number), the median is the average of the 5th and 6th terms in the ordered list.
- The 5th term is 46.
- The 6th term is 48.
Median=46+482=942=47.
Next, we calculate the absolute deviations of each score from the median (47):
- |34 - 47| = 13
- |38 - 47| = 9
- |42 - 47| = 5
- |44 - 47| = 3
- |46 - 47| = 1
- |48 - 47| = 1
- |54 - 47| = 7
- |55 - 47| = 8
- |63 - 47| = 16
- |70 - 47| = 23
Now, sum all the absolute deviations:
13+9+5+3+1+1+7+8+16+23=86.
Finally, we calculate the mean deviation by dividing the sum of absolute deviations by the number of scores (10):
Mean Deviation=8610=8.6.
The mean deviation about the median is 8.6.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Runs scored by a batsman in 10 innings are : 38, 70,48,34,42,55,63,46,54,44
The mean deviation isA8.6B6.4C10.6D9.6The scores of a batsman in 10 innings are 70,38,34,48,55,42,63,46,54,44. The mean deviation about medium is -
A7.6B8.6C8.2D8.4Find the mean deviation about median for the following data.
 A10.34B10.50C10.40D10.37
A10.34B10.50C10.40D10.37
The marks of 10 students in a class are 38, 70, 48,34 ,42, 55 63, 46, 54,44. Find the standard deviation of these marks.
View SolutionA batsman scores run in 10 innings as 38,70,48,34,42,55,63,46,54 and 44. The mean deviation about median is
(a)8.6
(b)6.4
(c)10.6
(d)7.6
View SolutionFind the mean deviation about the median for the data in Question

View SolutionFind the mean deviation about the median for the data in Question
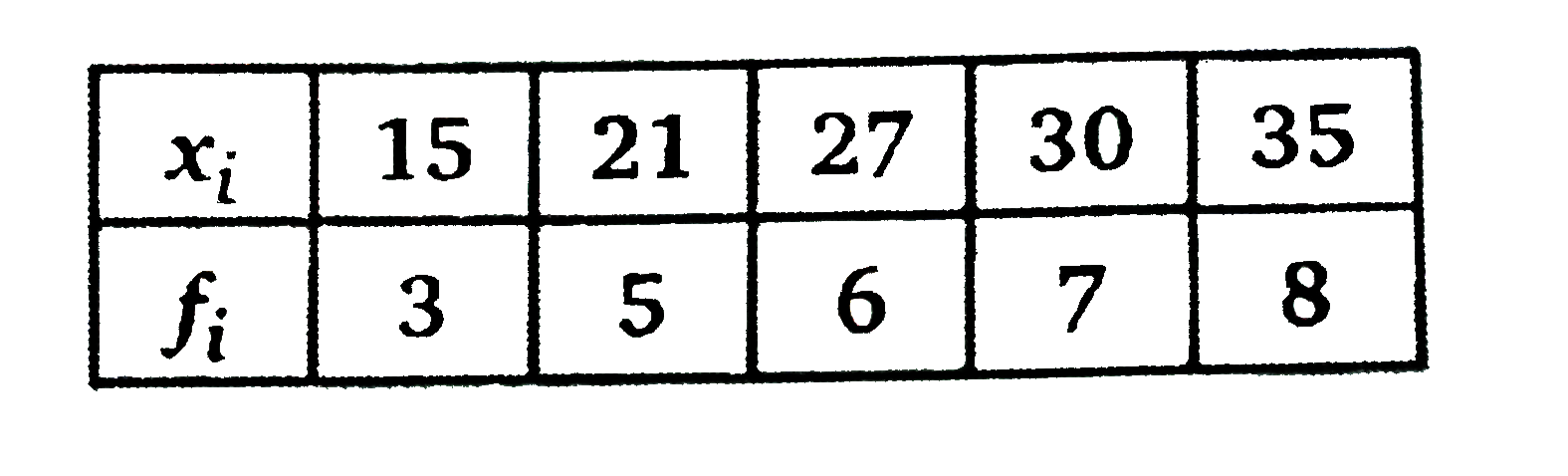
View SolutionFind the mean deviation about the median for the following data:
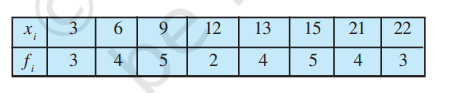
View Solution
