The set of points where the function f9x)=x|x| is differentiable is (−∞,∞) (b) (−∞,0)∪(0,∞) (0,∞) (d) [0,∞)
(−∞,∞)
(−∞,0)∪(0,∞)
(0,∞)
[0,∞)
The correct Answer is:A
We have, f(x)={x2,x≥0−x2,x<0
Clearly, f(x) is differentiable for all xgt0 and for all xlt0. so, we check the differentiable at x=0.
Now, (RHD at x=0)
(ddx(x)2)x=0=(2x)x=0=0
and (LHD at x=0)
(ddx(−x)2)x=0=(−2x)x=0=0
∴ (LHD at x=0)=(RHD at x=0)
so, f(x) is differentiable for all, x i.e., the set of all points where f(x) is differentiable is (−∞,∞).
Alternate solution:
It is clear from the graph f(x) is differentiable everywhere.
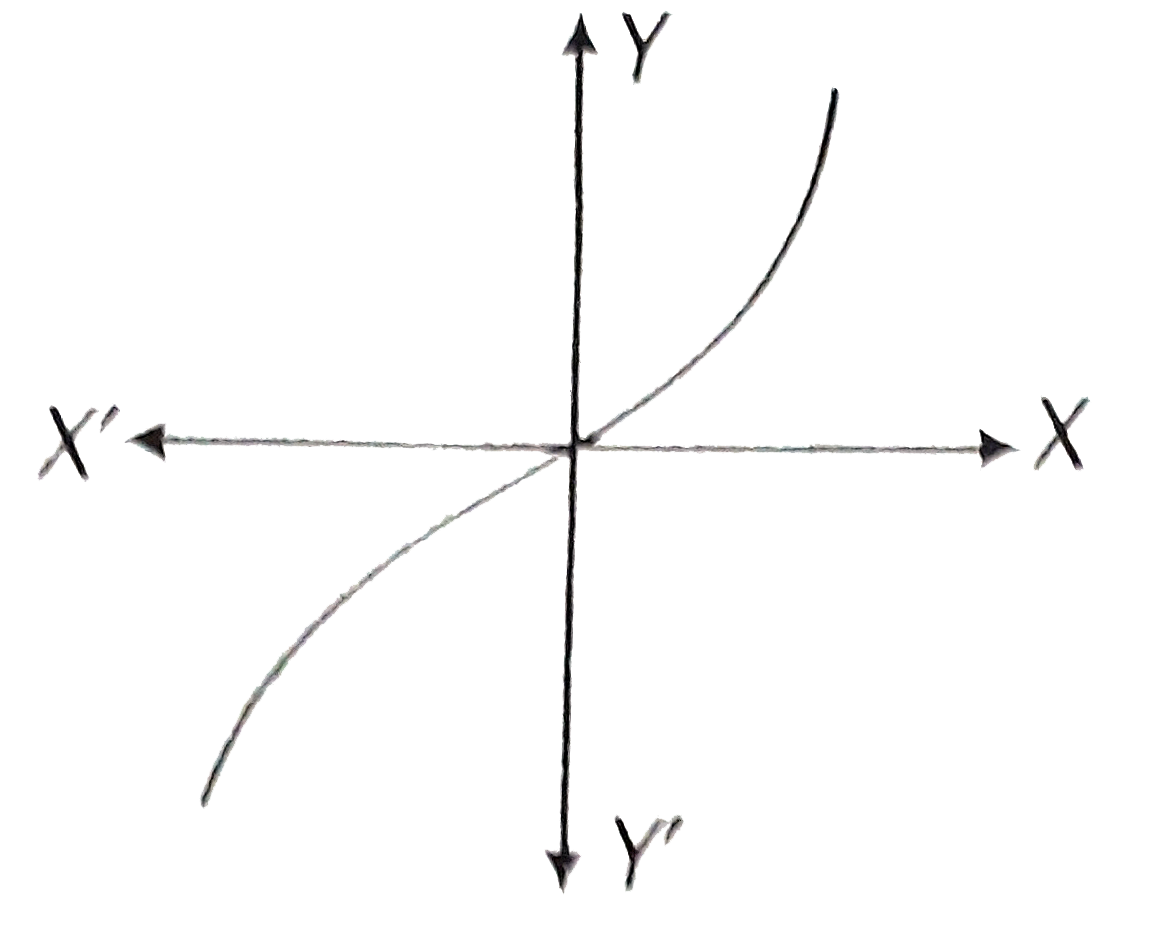
Topper's Solved these Questions
Similar Questions
The set of points where the function f(x)=x|x| is differentiable is (−∞,∞) (b) (−∞,0)∪(0,∞) (0,∞) (d) [0,∞)
View SolutionThe set of points where the function f(x)=x|x| is differentiable is (a) (−∞, ∞) (b) (−∞, 0)∪(0, ∞) (c) (0, ∞) (d) [0, ∞]
View SolutionThe function f(x)=x1+|x| is differentiable on (A) (0 oo) 0 oo) (B) (-oo 0) (C) (D) all the above
View SolutionThe function f(x)=11+x2 is decreasing in the interval
(i) (−∞,−1)
(ii) (−∞,0)
(iii) (1,∞)
(iv) (0,∞)
View SolutionThe range of the function f(x)=|x−1| is
A. (−∞,0)
B. [0,∞)
C. (0,∞)
D. R
View SolutionThe function f(x)=cot−1x+x increases in the interval (a) (1, ∞) (b) (−1, ∞) (c) (−∞, ∞) (d) (0, ∞)
View SolutionThe function f(x)=x9+3x7+64 is increasing on (a) R (b) (−∞, 0) (c) (0, ∞) (d) R0
View SolutionThe interval of increase of the function f(x)=x−ex+tan(2π/7) is (a) (0, ∞) (b) (−∞, 0) (c) (1, ∞) (d) (−∞, 1)
View SolutionThe domain of definition of the function f(x)=log|x| is R b. (−∞,0) c. (0,∞) d. R−{0}
View SolutionThe domain of the function f(x)=1√|x|−x is:
(A) (−∞,∞)
(B) (0,∞
(C) (−∞,0)
(D) (−∞,∞)-{0}
View Solution
