Question

The sets S and E are defined as given below:
${\displaystyle S=\{(x,y):|x-3|<1\text{and}|y-3|<1\}}$ and
${\displaystyle E=\{(x,y):4x^2+9y^2-32x-54y+109\le 0\}}$.
Show that ${\displaystyle S\subset E}$.

Explanation

Graph of S
`because |x-3|lt1implies-1lt(x-3)lt1implies2ltxlt4`
Similarly, `|y-3|lt1implies2ltylt4`
So, S consists of all points inside the square (not on `xne2`, 4 and `yne2`, 4) bounded by the lines x = 2, y = 2, x = 4 and y = 4.
Graph of R
`because 4x^(2)+9y^(2)-32x-54y+109le0`
`implies 4(x^(2)-8x)+9(y^(2)-6y)+109le0`
`implies 4(x-4)^(2)+9(y-3)^(2)le36`
`implies ((x-4)^(2))/(3^(2))+((y-3)^(2))/(2^(2))le1`
So, E consists of all points inside and on the ellipse with centre (4, 3) and semi-major and semi-minor axes are 3 and 2, respectively.

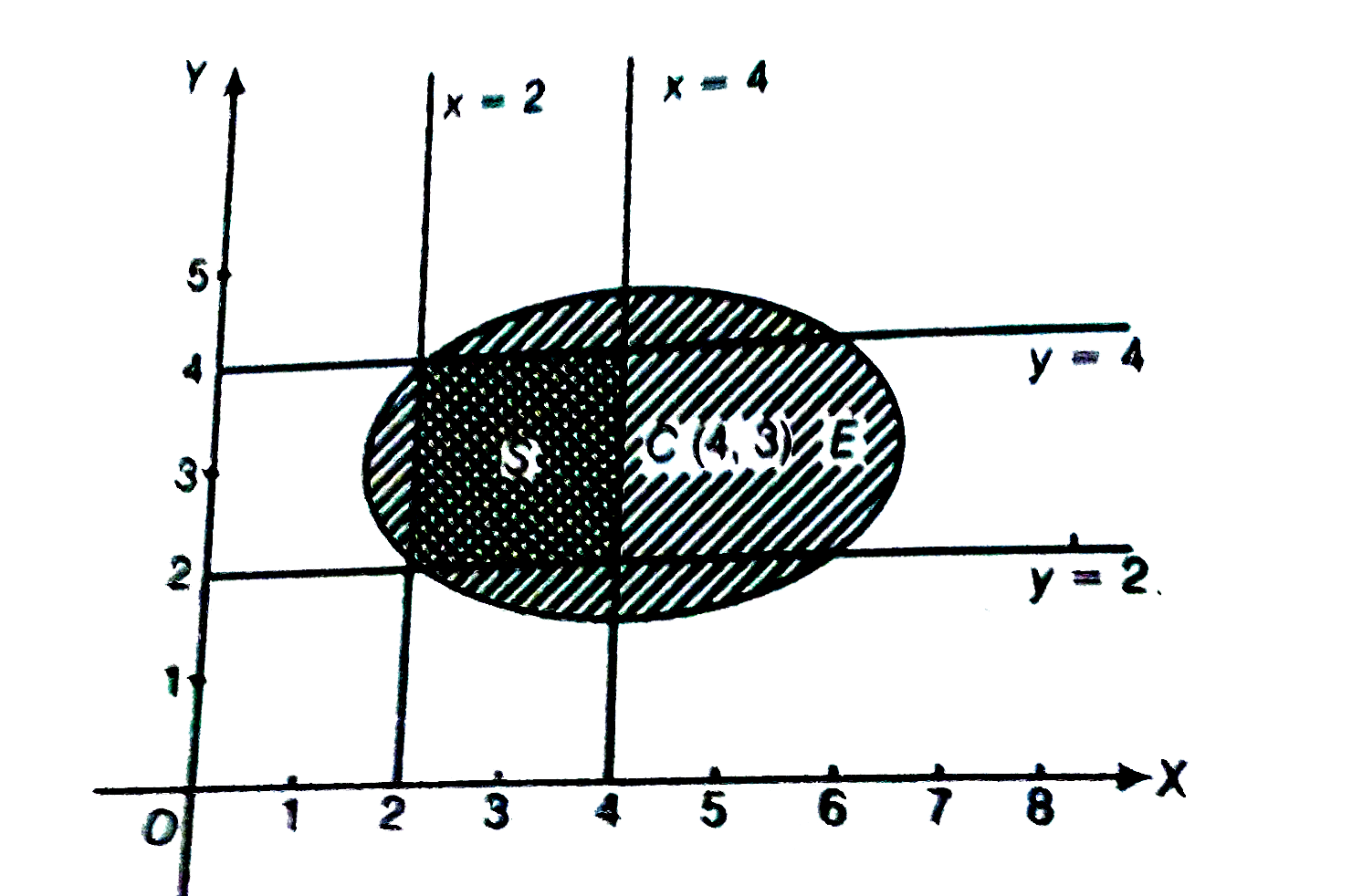
From the above graph, it is evident that the double hatched (which is S) is within the region represented by E. i.e., `SsubE`