The shortest distance between the lines $\frac{x - x_{1}}{a_{1}} = \frac{y - y_{1}}{b_{1}} = \frac{z - z_{1}}{c_{1}} and \frac{x - x_{2}}{a_{2}} = \frac{y - y_{2}}{b_{2}} = \frac{z - z_{2}}{c_{2}}$ is $∣ ∣ ∣ ∣ ∣ \begin{matrix} x_{1} - x_{1} & y_{2} - y_{1} & z_{2} - z_{1} a_{1} & b_{1} & c_{1} a_{2} & b_{2} & c_{2} \end{matrix} ∣ ∣ ∣ ∣ ∣$ /A Here, A refers to

A

${(b_{1} c_{2} - b_{2} c_{1})}_{1}^{2} - {(c_{1} a_{2} - c_{2} a_{1})}_{1}^{2} + {(a_{1} b_{2} - a_{2} b_{1})}_{1}^{2}$

B

${(b_{1} c_{2} - b_{2} c_{1})}_{1}^{2} + {(c_{1} a_{2} - c_{2} a_{1})}_{1}^{2} + {(a_{1} b_{2} - a_{2} b_{1})}_{1}^{2}$

C

$\sqrt{{(a_{1} b_{2} - a_{2} b_{1})}_{1}^{2} + {(b_{1} c_{2} - b_{2} c_{1})}_{1}^{2} + {(c_{1} a_{2} - c_{2} a_{1})}_{1}^{2}}$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The shortest distance between the line
$\frac{x - x_{1}}{a_{1}} = \frac{y - y_{1}}{b_{1}} = \frac{z - z_{1}}{c_{1}}$ and $\frac{x - x_{2}}{a_{2}} = \frac{y - y_{2}}{b_{2}} = \frac{z - z_{1}}{c_{1}}$ in cartesian froms is

|

Updated on:21/07/2023

Class 12 MATHS LINE

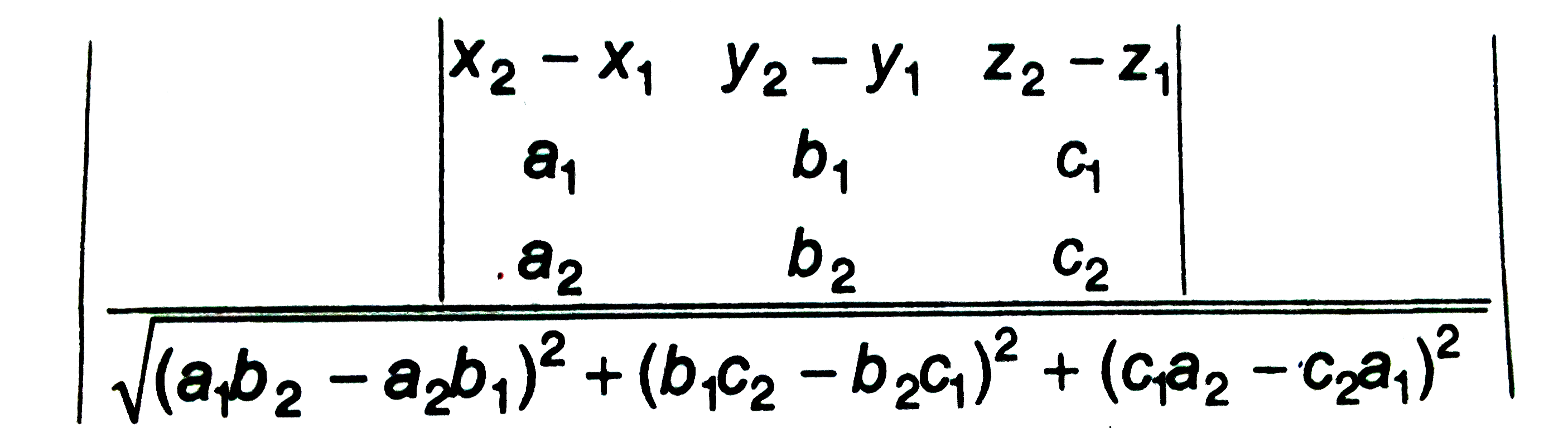
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If 2d is the shortest distance between the lines $x = 0, \frac{y}{b} + \frac{z}{c} = 1, y = 0, \frac{x}{a} - \frac{z}{c} = 1$ , then
A $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{d}$
B $\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} + \frac{1}{d^{2}} = 1$
C $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d} = 1$
D $\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} = \frac{1}{d^{2}}$
Question 2 - Select One
Cosnsider the system of equation
$a_{1} x + b_{1} y + c_{1} z = 0, a_{2} x + b_{2} y + c_{2} z = 0,$
$a_{3} x + b_{3} y + c_{3} z = 0$ if $∣ ∣ ∣ ∣ \begin{matrix} a_{1} & b_{1} & c_{1} a_{2} & b_{2} & c_{2} a_{3} & b_{3} & c_{3} \end{matrix} ∣ ∣ ∣ ∣ = 0$ , then the
system has
AMore than two solutions
BOne trivial and one-non trivial solutions
CNo solution
DOnly trivial solution (0,0,0)

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-LINE-MHT CET Corner

Home
Ask Doubt
Profile