The sides containing right angle of a right angled triangle are 8 cm and 6 cm. It is rotated about the side of 8 cm. Find the total surface area of the formed solid.
To find the total surface area of the solid formed by rotating a right-angled triangle about one of its sides, follow these steps:
Step 1: Identify the dimensions of the triangle
The right-angled triangle has sides of 8 cm and 6 cm. Here, 8 cm is the height (h) and 6 cm is the radius (r) when the triangle is rotated about the side of 8 cm.
Hint: Remember that when a triangle is rotated about one of its sides, that side becomes the height of the resulting cone.
Step 2: Determine the slant height of the cone
To find the slant height (l) of the cone formed, use the Pythagorean theorem:
l=√r2+h2
Substituting the values:
l=√62+82=√36+64=√100=10 cm
Hint: The slant height is the hypotenuse of the triangle formed by the radius and height.
Step 3: Calculate the total surface area of the cone
The total surface area (TSA) of a cone is given by the formula:
TSA=πr(r+l)
Substituting the values of r and l:
TSA=π×6×(6+10)=π×6×16=96π cm2
Hint: The total surface area includes the base area and the lateral surface area of the cone.
Final Answer
The total surface area of the solid formed is 96π cm2.
The right-angled triangle has sides of 8 cm and 6 cm. Here, 8 cm is the height (h) and 6 cm is the radius (r) when the triangle is rotated about the side of 8 cm.
To find the slant height (l) of the cone formed, use the Pythagorean theorem:
l=√r2+h2
Substituting the values:
l=√62+82=√36+64=√100=10 cm
The total surface area (TSA) of a cone is given by the formula:
TSA=πr(r+l)
Substituting the values of r and l:
TSA=π×6×(6+10)=π×6×16=96π cm2
The total surface area of the solid formed is 96π cm2.
Similar Questions
The sides containing right angles of a right angled triangle are 8 cm and 6 cm it is rotated about its hypotenuse . Find the volume and total surface area of the solid formed.
View SolutionThe sides containing right angles of a right angled triangle are 8 cm and 6 cm. It is rotated about its hypotenus. Find the volume and total surface area of the formed solid.
View SolutionA right triangle with sides 6 cm, 8 cm and 10 cm is revolved about the side 8 cm. Find the volume and the curved surface of the solid so formed.
View SolutionA right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm.Find the volume of the solid so obtained.
View SolutionIn a right angle, the sides conrtaining right angles are 5 cm and 12 cm. It is rotated aboutits hypotenuse taking it as axis. Find the volume of formed figure.
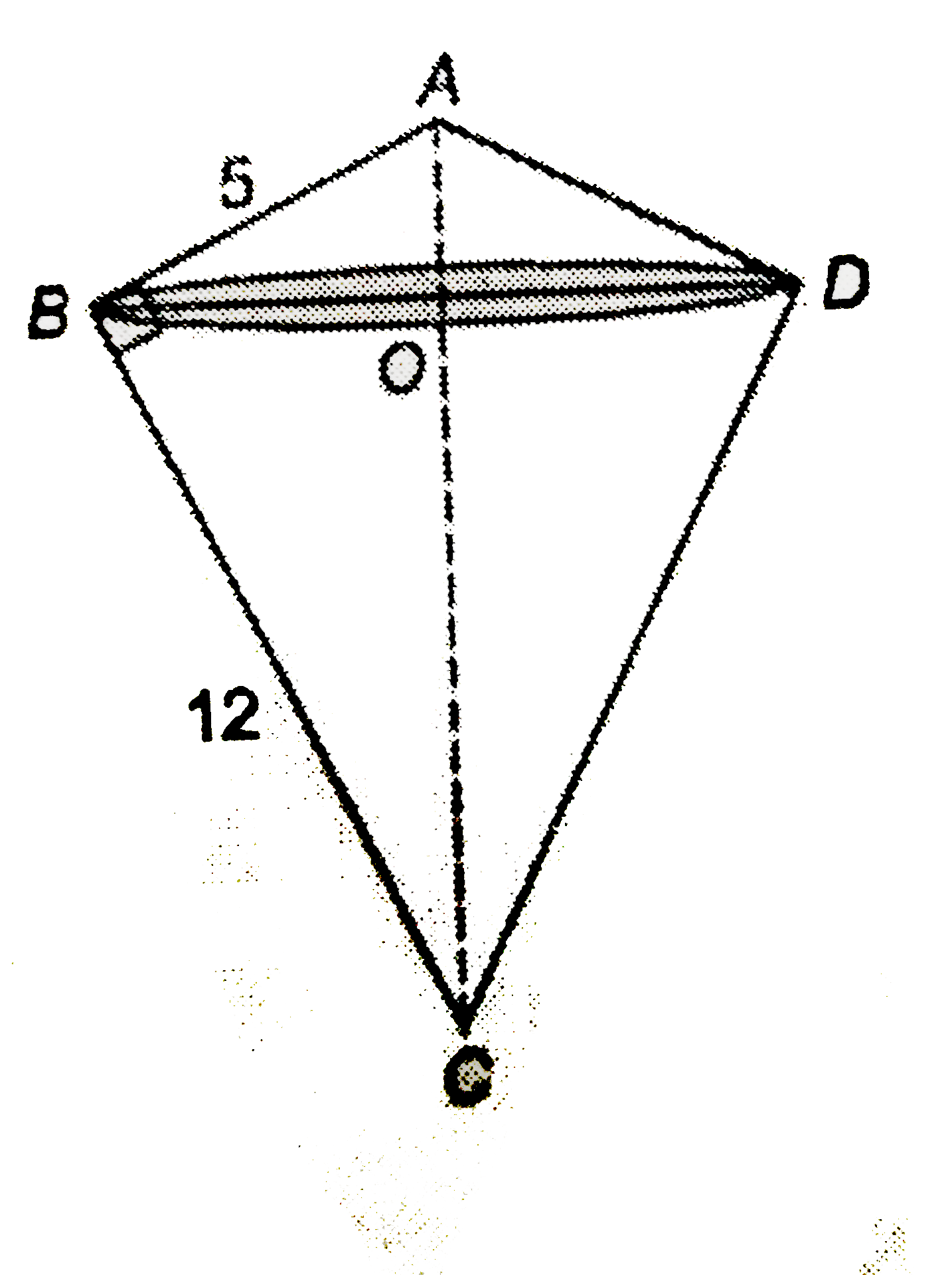
View SolutionA Right triangle whose sides are 15 cm and 20 cm; is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed.
View SolutionA right angle triangle with sides 3 cm and 4 cm is revolved around its hypotenuse . Find the volume of the double cone thus generated.
View SolutionThe area of a right-angled triangle is 54 sg. cm. If one of the two perpendicular sides is 9 cm, find the other.
View SolutionThe perimeter of a right angled triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
View SolutionA right angled triangle of which the sides containing the right angle are 6.3 cm and 10cm in length, is made to turn round on the longer side. Find the volume of the solid, thus generated. Also, find its curved surface area.
View Solution
