The sides of a right-angled triangle are integers. The length of one of the sides is 12. The largest possible radius of the incircle of such a triangle is-

A

2

B

3

C

4

D

5

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

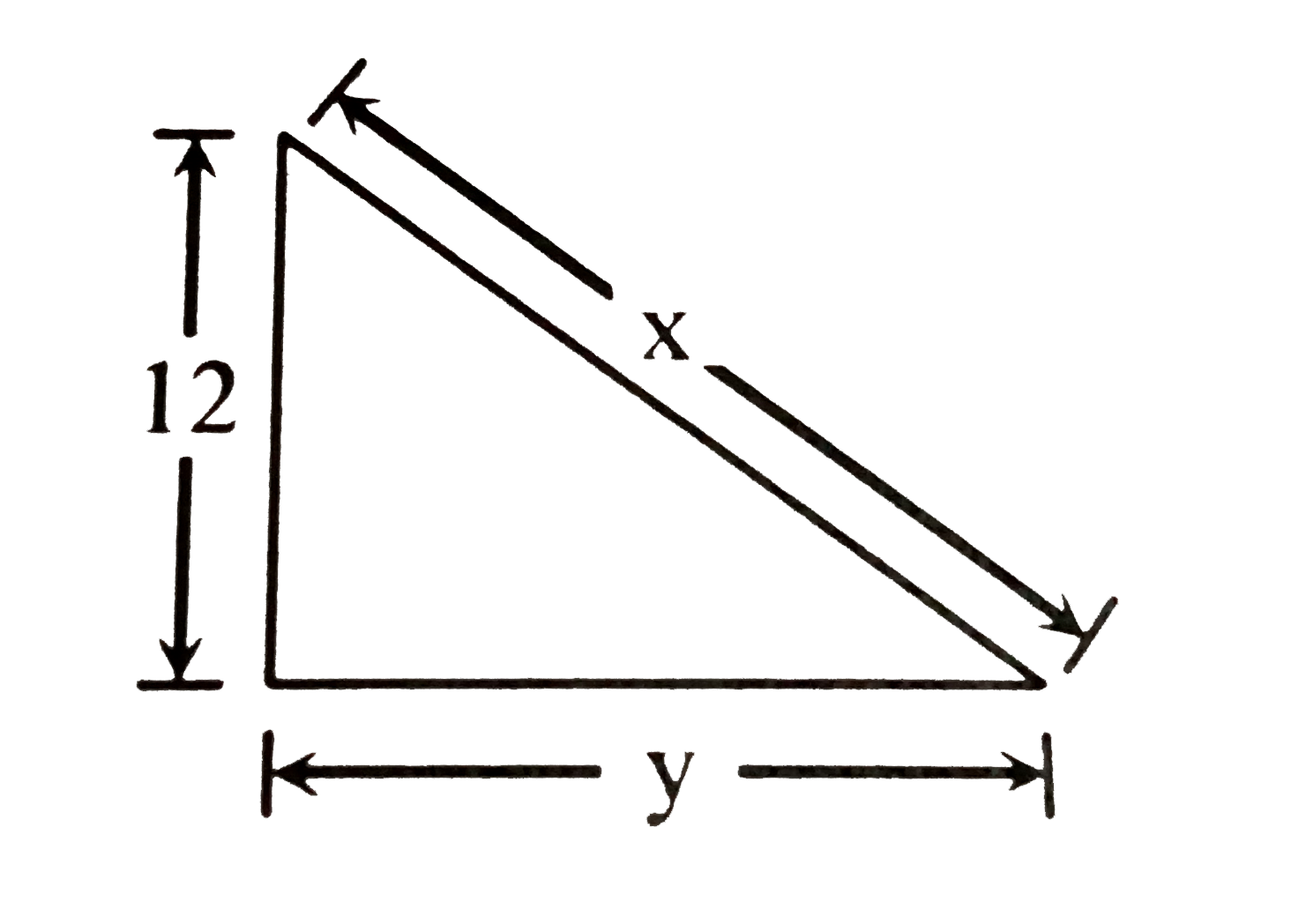
Clearly
$x^{2} - y^{2} = 144$
$(x - y) (x + y) = 144$
$x, y \in I$
So factorsize 144 into two even factors
x+y=72 x+y=36 x+y=18
x-y=2 s-y=9 x-y=8
x=37 x=20 x-13
y=35 y=16 y=5

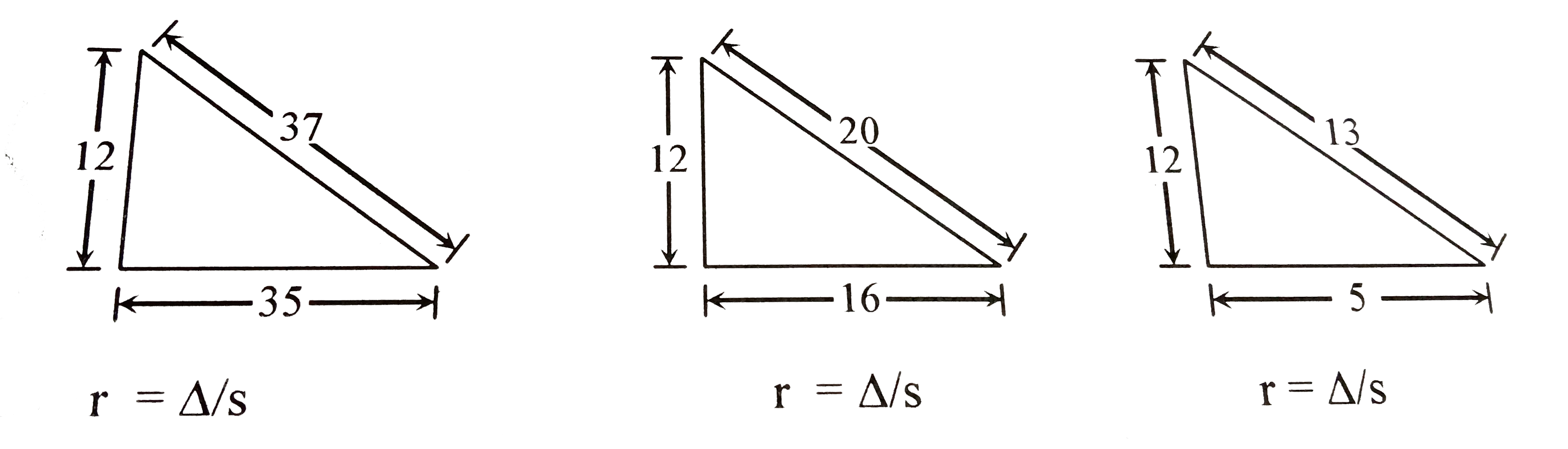
$r = Δ / s r = Δ / s r = Δ / s$
$r = \frac{1 / 2 \times 12 \times 35}{(\frac{12 + 35 + 37}{2})} r = \frac{1 / 2 \times 12 \times 16}{(\frac{16 + 20 + 12}{2})} r = 2$
$r = \frac{12 \times 35}{84} r = \frac{12 \times 16}{48}$
$r = 5 r = 4$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One or More
The sides of a right-angled triangle are consecutive integers. They are
A4, 5
B9, 10
C12, 13
D20, 21
Question 2 - Select One
If the sides of a right angled triangle are three consecutive integers, then the length of the smallest side is
Aa) 3 units
Bb) 2 units
Cc) 4 units
Dd) 5 units
Question 3 - Select One
If the length of sides of right angled triangle are in AP, then their ratio is
A $3 : 4 : 5$
B $2 : 3 : 4$
C $1 : 2 : 3$
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile