The slope of a line is double of the slope of another line. If tangent of the angle between them is 13, find the slopes of the lines.
To solve the problem step by step, we will denote the slopes of the two lines as m1 and m2. According to the problem, we know that:
1. The slope of one line m1 is double that of the other line m2:
m1=2m2
2. The tangent of the angle θ between the two lines is given as:
tan(θ)=13
The formula for the tangent of the angle between two lines with slopes m1 and m2 is given by:
tan(θ)=m2−m11+m1m2
Substituting the value of m1 into the formula:
tan(θ)=m2−2m21+2m2⋅m2
This simplifies to:
tan(θ)=−m21+2m22
Now, we can set this equal to the given value of tan(θ):
−m21+2m22=13
Next, we will cross-multiply to eliminate the fraction:
−3m2=1+2m22
Rearranging this equation gives us:
2m22+3m2+1=0
Now we will solve this quadratic equation using the factorization method. We can rewrite it as:
2m22+2m2+m2+1=0
Grouping the terms:
2m2(m2+1)+1(m2+1)=0
Factoring out (m2+1):
(2m2+1)(m2+1)=0
Setting each factor to zero gives us the possible values for m2:
1. 2m2+1=0 leads to m2=−12
2. m2+1=0 leads to m2=−1
Now we can find m1 for each case:
- If m2=−12:
m1=2m2=2(−12)=−1
- If m2=−1:
m1=2m2=2(−1)=−2
Thus, the slopes of the lines are:
1. m1=−1 and m2=−12
2. m1=−2 and m2=−1
Final Answer:
The slopes of the lines are:
- m1=−1 and m2=−12
- or m1=−2 and m2=−1
m1=2m2
tan(θ)=13
tan(θ)=m2−m11+m1m2
tan(θ)=m2−2m21+2m2⋅m2
This simplifies to:
tan(θ)=−m21+2m22
−m21+2m22=13
−3m2=1+2m22
2m22+3m2+1=0
2m22+2m2+m2+1=0
Grouping the terms:
2m2(m2+1)+1(m2+1)=0
Factoring out (m2+1):
(2m2+1)(m2+1)=0
1. 2m2+1=0 leads to m2=−12
2. m2+1=0 leads to m2=−1
- If m2=−12:
m1=2m2=2(−12)=−1
- If m2=−1:
m1=2m2=2(−1)=−2
1. m1=−1 and m2=−12
2. m1=−2 and m2=−1
The slopes of the lines are:
- m1=−1 and m2=−12
- or m1=−2 and m2=−1
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.220videos
STRAIGHT LINES
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.52videos
STRAIGHT LINES
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - MISCELLANEOUS EXERCISE24videos
STRAIGHT LINES
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.210videos
STATISTICS
- BOOK - NCERTCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE 3.17videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The slope of a line is 3 times the slope of the other line and the tangent of the angle between them is 4/13, sum of their slopes is equal to
A2B4C6D8 - Question 2 - Select One
Slope of a budget line is
AIncreaseing throghoutBDecreasing through outCConstant throughoutDFluctuating through out - Question 3 - Select One
The slope of the given line is ,
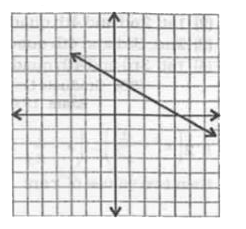 APositiveBNegativeCUndefinedDZero
APositiveBNegativeCUndefinedDZero


