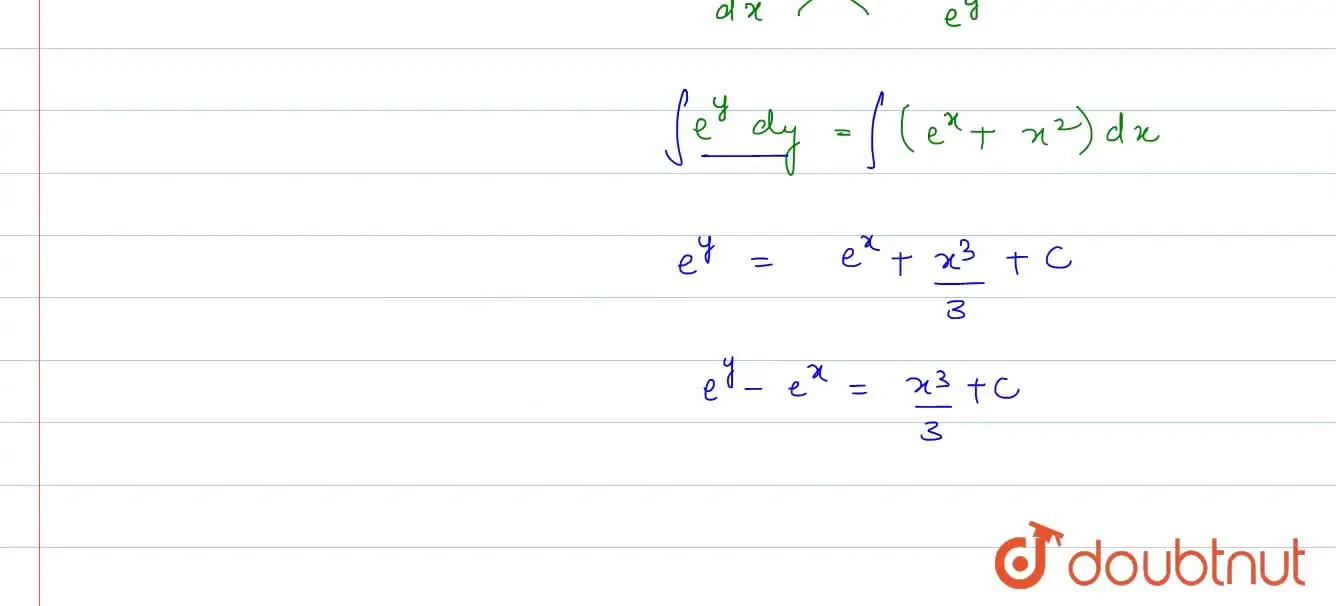The solution of differential equation dydx=ex−y+x2e−yis
A
y=ex−y−x2e−y+C
B
ey−ex=x33+C
C
ex+ey=x33+C
D
ex−ey=x33+C
Video Solution
Text Solution
The correct Answer is:B
Given that, dydx=ex−y+x2e−y
⇒dydx=exe−y+x2e−y
⇒dydx=ex2+x2ey
On integrating both sides, we get
∫eydy=∫(ex+x2)dx
⇒ey=ex+x33+C⇒ey−ex=x33+C
|
Updated on:21/07/2023
Related Playlists
Similar Questions
The solution of the differential equation dydx=ex−y+x2e−y is (A) y=ex+12x2+c (B) ey−x=13x3+c (C) ey=ex+13x3+c (D) none of these
View SolutionThe solution of the differential equation dydx=ex+y+x2ey is
View Solutionsolution of differential equation dydx=x+exy
View SolutionThe solution of the differential equation dydx=ex−y+x2e−y is :
View SolutionThe solution of the differential equation dydx=ex−y+x2e−y is :
View SolutionThe solution of the differential equation
dydx=e3x−2y+x2e−2y,isView Solutionwhat is the solution of the differential equation
dydx=ex−y(ey−x−ey) ?View SolutionThe solution of the differential equation
dydx=ex−y(ex−ey) isView SolutionThe solution of the differential equation
dydx=ex−y(ex−ey) isView SolutionThe solution of the differential equation dydx=ey+x+ey−x, is
View Solution