The solution of the differential equaiton

A

$\frac{d y}{d x} + y tan x = sec x,$ is

B

$y sec x = tan x + C$

C

$y tan x = sec x + C$

D

$tan x = y tan x + C$

Text Solution

Verified by Experts

The correct Answer is:A

|

Updated on:21/07/2023

Class 12 MATHS DIFFERENTIAL EQUATIONS

Topper's Solved these Questions

BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise
74videos
DIFFERENTIAL EQUATIONS
BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26videos
DERIVATIVE AS A RATE MEASURER
BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Exercise
17videos
DIFFERENTIALS, ERRORS AND APPROXIMATIONS

Similar Questions

Knowledge Check

Question 1 - Select One
The general solution of the differential equaiton $(1 + y^{2}) d x + (1 + x^{2}) d y = 0$ , is
A $x - y = C (1 - x y)$
B $x - y = C (1 + x y)$
C $x + y = C (1 - x y)$
D $x + y = C (1 + x y)$
Question 2 - Select One
The solution of differential equation
$\frac{d t}{d x} = \frac{t [\frac{d}{d x} {g (x)}] - t^{2}}{g (x)}$ is
A $t = \frac{g (x) + C}{x}$
B $t = \frac{g (x)}{x} + C$
C $t = \frac{g (x)}{x + C}$
D $t = g (x) + x + C$
Question 3 - Select One
Solution of differential equation

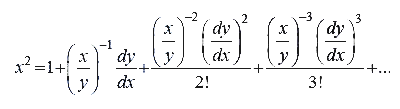A $y^{2} = x^{2} ({ln}^{2} - 1) + C$
B $y = x^{2} (ln x - 1) + C$
C $y^{2} = x (ln x - 1) + C$
D $y = x^{2} e^{x^{2}} + C$

OBJECTIVE RD SHARMA-DIFFERENTIAL EQUATIONS-Chapter Test

Home
Ask Doubt
Profile