The solution of the system of equations x+(cosα)y=1and(cosα)x+4y=2 satisfy x≥45 and y≤12, then the value of α can lie in the inverval
α∈[π4,π3]
α∈[0,π6]
α∈[π6,π3]
α∈[π3,π2]
The correct Answer is:D
To solve the system of equations given by:
1. x+(cosα)y=1
2. (cosα)x+4y=2
we will use Cramer's rule to find the values of x and y in terms of α.
Step 1: Write the Coefficient Matrix
The coefficient matrix A is given by:
A=(1cosαcosα4)
Step 2: Calculate the Determinant of A
The determinant Δ of the matrix A is calculated as:
Δ=1⋅4−(cosα)(cosα)=4−cos2α
Step 3: Calculate Δ1 and Δ2
Now we calculate Δ1 and Δ2:
- For Δ1, replace the first column with the right-hand side values:
Δ1=∣∣∣1cosα24∣∣∣=1⋅4−2⋅cosα=4−2cosα
- For Δ2, replace the second column with the right-hand side values:
Δ2=∣∣∣11cosα2∣∣∣=1⋅2−1⋅cosα=2−cosα
Step 4: Find x and y
Using Cramer's rule:
x=Δ1Δ=4−2cosα4−cos2α
y=Δ2Δ=2−cosα4−cos2α
Step 5: Apply the Given Conditions
We have the conditions:
1. x≥45
2. y≤12
Condition 1: x≥45
4−2cosα4−cos2α≥45
Cross-multiplying gives:
5(4−2cosα)≥4(4−cos2α)
Expanding both sides:
20−10cosα≥16−4cos2α
Rearranging gives:
4cos2α−10cosα+4≥0
Condition 2: y≤12
2−cosα4−cos2α≤12
Cross-multiplying gives:
2(2−cosα)≤4−cos2α
Expanding both sides:
4−2cosα≤4−cos2α
Rearranging gives:
cos2α−2cosα≥0
Factoring gives:
cosα(cosα−2)≥0
Step 6: Solve the Inequalities
1. From 4cos2α−10cosα+4≥0, use the quadratic formula to find the roots:
cosα=10±√100−648=10±68
This gives cosα=2 and cosα=12.
2. From cosα(cosα−2)≥0, the solution is cosα≤0 or cosα≥2 (not possible since cosα cannot exceed 1).
Step 7: Determine the Interval for α
The valid range for α based on cosα is:
12≤cosα≤1
This corresponds to the angles:
α∈(π3,π2)
Final Answer
Thus, the value of α can lie in the interval:
(π3,π2)
2. (cosα)x+4y=2
The coefficient matrix A is given by:
A=(1cosαcosα4)
The determinant Δ of the matrix A is calculated as:
Δ=1⋅4−(cosα)(cosα)=4−cos2α
Now we calculate Δ1 and Δ2:
Δ1=∣∣∣1cosα24∣∣∣=1⋅4−2⋅cosα=4−2cosα
Δ2=∣∣∣11cosα2∣∣∣=1⋅2−1⋅cosα=2−cosα
Using Cramer's rule:
x=Δ1Δ=4−2cosα4−cos2α
y=Δ2Δ=2−cosα4−cos2α
We have the conditions:
1. x≥45
2. y≤12
4−2cosα4−cos2α≥45
Cross-multiplying gives:
5(4−2cosα)≥4(4−cos2α)
Expanding both sides:
20−10cosα≥16−4cos2α
Rearranging gives:
4cos2α−10cosα+4≥0
2−cosα4−cos2α≤12
Cross-multiplying gives:
2(2−cosα)≤4−cos2α
Expanding both sides:
4−2cosα≤4−cos2α
Rearranging gives:
cos2α−2cosα≥0
Factoring gives:
cosα(cosα−2)≥0
1. From 4cos2α−10cosα+4≥0, use the quadratic formula to find the roots:
cosα=10±√100−648=10±68
This gives cosα=2 and cosα=12.
The valid range for α based on cosα is:
12≤cosα≤1
This corresponds to the angles:
α∈(π3,π2)
Thus, the value of α can lie in the interval:
(π3,π2)
Topper's Solved these Questions
Similar Questions
Knowledge Check
The solution of the system of equations is x−y+2z=1,2y−3z=1 and 3x−2y+4y=2 is
Ax=1,y=5 and z=3Bx=0,y=5 and z=3Cx=0,y=5 and z=−3DNone of the aboveThe solution of the system of equations 3x+2y≤12,x≥1,y≤2 is
A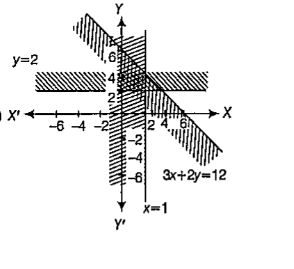 B
B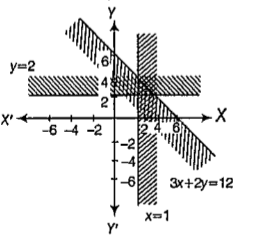 C
C DNone of the above
DNone of the aboveFind the real solution of the system of equations.
x4+y4−x2y2=13
And x2−y2+2xy=1
Satisfying the condition xy≥0A(x=1,y=−2),(x=−1,y=2)B(x=2,y=1),(x=−2,y=−1)C(x=1,y=2),(x=−1,y=−2)D(x=1,y=−2),(x=−1,y=−2)
The number of solutions of the system of equations: 2x+y−z=7, x−3y+2z=1, x+4y−3z=5 is (a) 3 (b) 2 (c) 1 (d) 0
View SolutionDraw the graph of the solution set of the system of inequations 2x+3y≤4,x≥0andy≥0.
View SolutionThe values of x satisfying the system of equations 2sinx−cosy=1,16sin2x+cos2y=4 are given by :
View SolutionThe system of lienar equations
x−y+z=1
x+y−z=3
x−4y+4z=α has
View SolutionThe most general values of x satisfying the equation sinx=sinαandcosθ=cosα is
View Solution
