The sums of n,2n,3n terms of an A.P. are S1,S2,S3 respectively.
Prove that : S3=3(S2−S1) Solution in Kannada
The correct Answer is:=3n2[2a+(3d−1)d]=S3 =L.H.S.
Step by step video, text & image solution for The sums of n, 2n , 3n terms of an A.P. are S_(1) , S_(2) , S_(3) respectively. Prove that : S_(3) = 3 (S_(2) - S_(1) ) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - TEXTUAL EXERCISE (Exercise 1.1)4videos
ARITHMETIC PROGRESSIONS
- BOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - TEXTUAL EXERCISE (Exercise 1.2)20videos
ARITHMETIC PROGRESSIONS
- BOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - TO FIND THE NTH TERM OF AN A.P. (ILLUSTRATIVE EXAMPLES)11videos
ARITHMETIC PROGRESSIONS
- BOOK - ZEN PUBLICATIONCHAPTER - AREA RELATED TO CIRCLES EXERCISE - ADDITIONAL QUESTIONS (HIGHER ORDER THINKING SKILLS)7videos
AREA RELATED TO CIRCLES
- BOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)9videos
CIRCLES
Similar Questions
In which of the following situations, does the list of numbers involved make arithmetic progression, and why ?
The taxi fare after each km when fare is Rs. 15 for the first km and Rs.8 for each additional km.02:19View SolutionFill in the blanks in the following table, given that a is the first term, d the common difference and an nth term of the AP :
 03:49View Solution
03:49View SolutionHow many two digit numbers are divisible by 3?
05:38View SolutionFind the area of the shaded region portion in the given figure if E is the midpoint of AB,AGE and BEF are quadrants, and DOC is a semicircle.
 04:01View Solution
04:01View SolutionIn the adjoining figure, XY is a diameter of the circle and PQ is a tangent to the circle at Y. Given that ⌊AXB=50∘ and ⌊ABX=70∘, calculate ⌊BAY and ⌊APY.
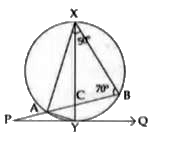 06:51View Solution
06:51View SolutionLet the sum of n, 2n, 3n terms of an A.P. be S1,S2and S3, respectively, show that S3=3(S2−S1).
03:12View SolutionThe sum of n,2n,3n terms of an A.P.are S_(1),S_(2),S_(3) respectively.Prove that S_(3)=3(S_(2)-S_(1))
05:42View SolutionIf S_(1),S_(2),S_(3) be respectively the sums of n,2n and 3n terms of a G.P.,prove that S_(1)(S_(3)-S_(2))=(S_(2)-S_(1))^(2)
04:11View SolutionIf the sum of n,2n,3n terms of an AP are S_(1),S_(2),S_(3) respectively.Prove that S_(3)=3(S_(2)-S_(1))
04:12View SolutionIf S1,S2,S3 be respectively the sums of n,2n,3n terms of a G.P., then prove that (S1)2+(S2)2=S1(S2+S3) .
06:24View SolutionThe sum of n,2n,3n terms of an A.P. are S1S2,S3, respectively. Prove that S3=3(S2−S1).
04:55View Solutionयदि गुणोत्तर श्रेणी के n, 2n और 3n पदों के योगफल क्रमशः S1,S2 और S3 है, तो सिद्ध करो कि
S1(S3−S2)=(S2−S1)2View Solutionयदि किसी A.P. के प्रथम n , 2n, 3n पदों के योग क्रमशः S1,S2 और S3 हो , तो दिखाएँ कि S3=3(S2−S1)
04:29View SolutionIf S1,S2,S3 be respectively the sums of n, 2n and 3n terms of a G.P., prove that, S1(S3−S2)=(S2−S1)2.
03:00View Solutionयदि गु० श्रे० के n,2n,3n पदों का योग क्रमशः S1,S2,S3 हों तो सिद्ध करें की S21+S22=S1(S2+S3).
05:38View Solution
