The tangents drawn from a point P to ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ make angles $α and β$ with the major axis, Now, match the following lists :

Text Solution

Verified by Experts

The equation of any tangent to
$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (1)$
is given by
$y = m x + \sqrt{a^{2} m^{2} + b^{2}}$

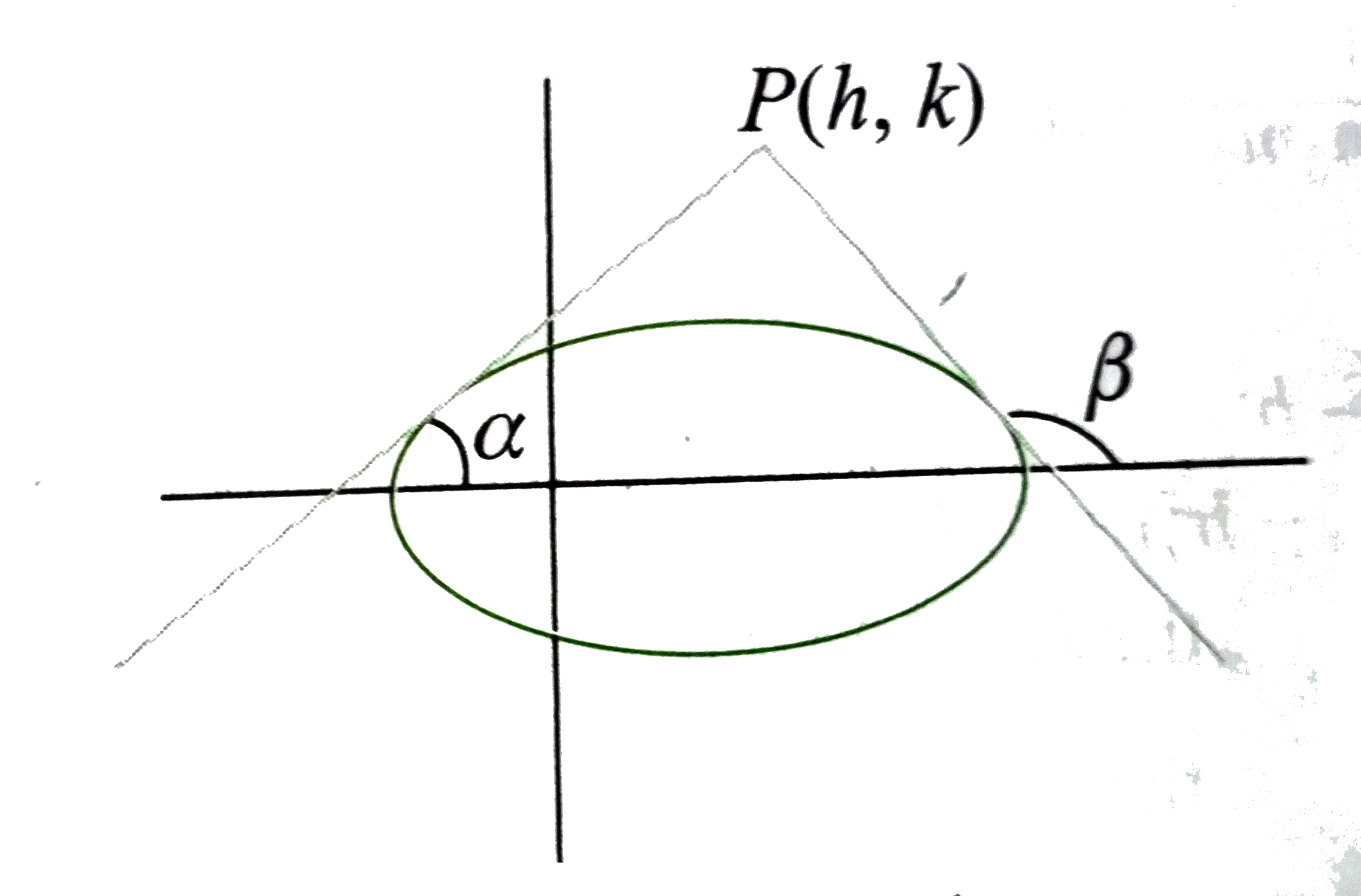
Sinc the passes through P(h,k) we have
$k = m h + \sqrt{a^{2} m^{2} + b^{2}}$
or $m^{2} (h - a^{12}) - 2 k m n h + + (k^{2} + b^{2}) = 0 (2)$
As (2) is quadratic in m, having two roots $m_{1} and m_{2}$ (ay), we age
$m_{1} + m_{2} = \frac{2 h k}{h^{2} - a^{2}}, m_{1} m_{2} = \frac{k^{2} - b^{2}}{h^{2} - a^{2}} (3)$
or $tan (α + β) = \frac{tan α + tan β}{1 - tan α tan β}$
$= \frac{m_{1} + m_{2}}{1 - m_{1} m_{2}} = \frac{2 h k / (h^{2} - a^{2})}{1 - {(k l^{2} - b^{2}) / (h^{2} - a^{2})}} = \frac{2 h k}{h^{2} - k^{2} - a^{2} + b^{2}}$
(a) $α + β = \frac{c π}{2}$ ltbrtgt When c even,
$m_{1} + m_{2} = 0$
$\frac{2 k h}{h^{2} - a^{2}} = 0$
or $2 k h = 0$
$x y = 0$
Which is the equation of a pair of straight lines.
Whnen c is odd,
$1 - m_{1} m_{2} = 0$
$or \frac{k^{2} - b^{2}}{h^{2} - a^{2}} = 1$
Therefore, the locus of (h,k) is $y^{2} - b^{2} = x^{2} - a^{2}$
which is a hyperbola.
(b) $m_{1} m_{2} = c$
or $\frac{k^{2} - b^{2}}{h^{2} - a^{2}} = c$
when $c = 0, k = \pm b$ , the locus is a pair of straigth lines.
When $c = 1, h^{2} - k^{2} = a^{2} - b^{2}$ , the locusb is a hyperbola.
When $c - 1, h^{2} + k^{2} = a^{2} + b^{2},$ the locus is a circle
When $c = - 2, 2 h^{2} + k^{2} = 2 a^{2} + b^{2}$ , the locus is an ellipse
(c) $tan α + β = c$
or $m_{1} + m_{2} = c$
When $c = 0, k h, 2 - k h = 0$ , the locus ia pair of straight lines,
When $c \neq 0$
$c (h^{2} - a^{2}) - 2 k h = 0$
the locus of (h,k) is $c x^{2} - 2 k h = 0$
$D η = - c a^{2} \neq 0$
Also, $h^{2} - a b = > 0$
Therefore, the locus is a hyperboal or $c \neq = 0$
(d) $cot α + cos β = c$
or $\frac{1}{m_{1}} + \frac{1}{m_{2}} = c$
or $\frac{m_{1} + m_{2}}{m_{1} m_{2}} = c$
or $\frac{2 k h}{k^{2} - b^{2}} = c$
When c=0, the locus is pair of straigth lines
Wehn $c \neq 0$ , the locus is hyperbola (as in previous case c)

If the tangents drawn from a point on the hyperbola $x^{2} - y^{2} = a^{2} - b^{2}$ to ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ make angle $α$ and $β$ with the transverse axis of the hyperbola, then
A $tan α - tan β = 1$
B $tan α + tan β = 1$
C $tan α tan β = 1$
D $tan α tan β = - 1$
Two tangents are drawn from a point on hyperbola $x^{2} - y^{2} = 5$ to the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ . If they make angle $α and β$ with x-axis, then
A $α - β = \pm \frac{π}{2}$
B $α + β = \frac{π}{2}$
C $α + β = π$
D $α + β = 0$