The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is 315rs and for a journey of 15km, the charge paid is 465rs. What are the fixed charges and the charge per kilometre ? How much does a person have to pay for travelling a distance of 32km ?
The correct Answer is:975rs
To solve the problem of taxi charges, we will set up a system of equations based on the information provided. Let's break it down step by step.
Step 1: Define Variables
Let:
- x = fixed charge (in rupees)
- y = charge per kilometer (in rupees)
Step 2: Set Up the Equations
From the information given:
1. For a distance of 10 km, the total charge is 315 rupees:
x+10y=315(Equation 1)
2. For a distance of 15 km, the total charge is 465 rupees:
x+15y=465(Equation 2)
Step 3: Solve the Equations
We can solve these equations simultaneously. First, we can express x from Equation 1:
x=315−10y(Substituting into Equation 2)
Now, substitute this expression for x into Equation 2:
(315−10y)+15y=465
Step 4: Simplify and Solve for y
Combine like terms:
315−10y+15y=465
315+5y=465
Now, isolate y:
5y=465−315
5y=150
y=1505=30
Step 5: Substitute y Back to Find x
Now that we have y, we can find x:
x=315−10⋅30
x=315−300=15
Step 6: Summary of Charges
- Fixed charge x=15 rupees
- Charge per kilometer y=30 rupees
Step 7: Calculate Charge for 32 km
To find out how much a person has to pay for traveling a distance of 32 km:
Total charge=x+32y
Total charge=15+32⋅30
=15+960=975
Final Answer
The fixed charge is 15 rupees, the charge per kilometer is 30 rupees, and the total charge for traveling 32 km is 975 rupees.
---
Let:
- x = fixed charge (in rupees)
- y = charge per kilometer (in rupees)
From the information given:
1. For a distance of 10 km, the total charge is 315 rupees:
x+10y=315(Equation 1)
2. For a distance of 15 km, the total charge is 465 rupees:
x+15y=465(Equation 2)
We can solve these equations simultaneously. First, we can express x from Equation 1:
x=315−10y(Substituting into Equation 2)
(315−10y)+15y=465
Combine like terms:
315−10y+15y=465
315+5y=465
5y=465−315
5y=150
y=1505=30
Now that we have y, we can find x:
x=315−10⋅30
x=315−300=15
- Fixed charge x=15 rupees
- Charge per kilometer y=30 rupees
To find out how much a person has to pay for traveling a distance of 32 km:
Total charge=x+32y
Total charge=15+32⋅30
=15+960=975
The fixed charge is 15 rupees, the charge per kilometer is 30 rupees, and the total charge for traveling 32 km is 975 rupees.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SIMULTANEOUS LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Topic 2 (3 Marks questions)12videos
SIMULTANEOUS LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)13videos
SIMULTANEOUS EQUATIONS
- BOOK - ICSECHAPTER - SOLIDSEXERCISE - Exercise 21(C )10videos
SOLIDS
Similar Questions
The taxi charges in a city comprise of a fixed charge together with the charge for the distance covered. For a journey of 10 km the charge paid is Rs 75 and for a journey of 15 km the charge paid is Rs 110. What will a person have to pay for travelling a distance of 25 km?
View SolutionThe car hire charges in a city comprise of a fixed charges together with the charge for the distance covered. For a journey of 12 km, the charge paid is Rs 89 and for a journey of 20 km, the charge paid is Rs 145. What will a person have to pay for travelling a distance of 30 km?
View SolutionThe force between two charges 4C and -2C which are separated by a distance of 3km is
View SolutionFor 100 km, a taxi charges Rs. 1,800. How much will it charge for a journey of 120 km ?
View SolutionA lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid Rs 27 for a book kept for seven days, while Susy paid Rs 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionThe force between two similar charges of magnitude 2C each separated by a distance 2km
View SolutionTwo fixed charges 4Q (positive) and Q (negative) are located at A and B. the distance AB being 3 m.
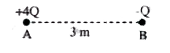 View Solution
View SolutionA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and at a distance 2L apart so that distance of this charge from each charge located at end is L. Assuming that the middle charge moves along the line joining the fixed charges. The frequency of oscillation when it is displaced slightly is
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View Solution

