The three sides of a trapezium are equal, each being 6 cm long, find the area of the trapezium when it is maximum.
The correct Answer is:27√3 sq. cm
To find the maximum area of a trapezium with three equal sides of length 6 cm, we can follow these steps:
Step 1: Understand the trapezium configuration
Given that three sides of the trapezium are equal (each measuring 6 cm), we can denote the lengths of the sides as follows:
- Let the lengths of the two non-parallel sides be a=6 cm each.
- Let the length of the parallel side (the base) be b.
Step 2: Express the area of the trapezium
The area A of a trapezium can be expressed as:
A=12×(b1+b2)×h
where b1 and b2 are the lengths of the two parallel sides and h is the height. In our case, we can consider one of the bases as b and the other base as 6 cm (the length of the equal sides).
Step 3: Relate the height to the sides
To find the height h, we can use the Pythagorean theorem. The height can be expressed in terms of x, where x is the distance from the top vertex to the foot of the height:
h=√62−x2=√36−x2
Step 4: Set up the area function
The area can now be expressed in terms of x:
A=12×(b+6)×h
Substituting h:
A=12×(b+6)×√36−x2
Step 5: Find the maximum area
To maximize the area, we can differentiate A with respect to x and set the derivative to zero:
1. Differentiate A with respect to x:
dAdx=12((b+6)⋅ddx(√36−x2))
Using the chain rule:
ddx(√36−x2)=−x√36−x2
Thus,
dAdx=12(b+6)⋅−x√36−x2
2. Set dAdx=0:
This implies:
x=0orb+6=0(not possible)
Step 6: Evaluate the area at critical points
When x=0:
h=√36−02=6
The area becomes:
A=12×(6+6)×6=12×12×6=36 cm2
Step 7: Conclusion
The maximum area of the trapezium occurs when x=0 and is given by:
Maximum Area=36 cm2
Given that three sides of the trapezium are equal (each measuring 6 cm), we can denote the lengths of the sides as follows:
- Let the lengths of the two non-parallel sides be a=6 cm each.
- Let the length of the parallel side (the base) be b.
The area A of a trapezium can be expressed as:
A=12×(b1+b2)×h
where b1 and b2 are the lengths of the two parallel sides and h is the height. In our case, we can consider one of the bases as b and the other base as 6 cm (the length of the equal sides).
To find the height h, we can use the Pythagorean theorem. The height can be expressed in terms of x, where x is the distance from the top vertex to the foot of the height:
h=√62−x2=√36−x2
The area can now be expressed in terms of x:
A=12×(b+6)×h
Substituting h:
A=12×(b+6)×√36−x2
To maximize the area, we can differentiate A with respect to x and set the derivative to zero:
1. Differentiate A with respect to x:
dAdx=12((b+6)⋅ddx(√36−x2))
Using the chain rule:
ddx(√36−x2)=−x√36−x2
Thus,
dAdx=12(b+6)⋅−x√36−x2
This implies:
x=0orb+6=0(not possible)
When x=0:
h=√36−02=6
The area becomes:
A=12×(6+6)×6=12×12×6=36 cm2
The maximum area of the trapezium occurs when x=0 and is given by:
Maximum Area=36 cm2
Topper's Solved these Questions
- MODEL TEST PAPER - 3 BOOK - ICSECHAPTER - MODEL TEST PAPER - 3 EXERCISE - SECTION - B
10 Videos
- MODEL TEST PAPER - 3 BOOK - ICSECHAPTER - MODEL TEST PAPER - 3 EXERCISE - SECTION - C
10 Videos
- MODEL TEST PAPER - 2BOOK - ICSECHAPTER - MODEL TEST PAPER - 2EXERCISE - Section - C
10 Videos
- MODEL TEST PAPER - 4BOOK - ICSECHAPTER - MODEL TEST PAPER - 4EXERCISE - SECTION - C
10 Videos
Similar Questions
The three sides of a trapezium are equal, each being 8cm. The area of the trapezium, where it is maximum, is (a)24√3 cm2 (b) 48√3cm2 (c)72√3cm2 (d) none of these
View SolutionIf the length of three sides of a trapezium other than the base is 10cm each, find the area of the trapezium, when it is maximum.
View SolutionFind the area of the given trapezium.
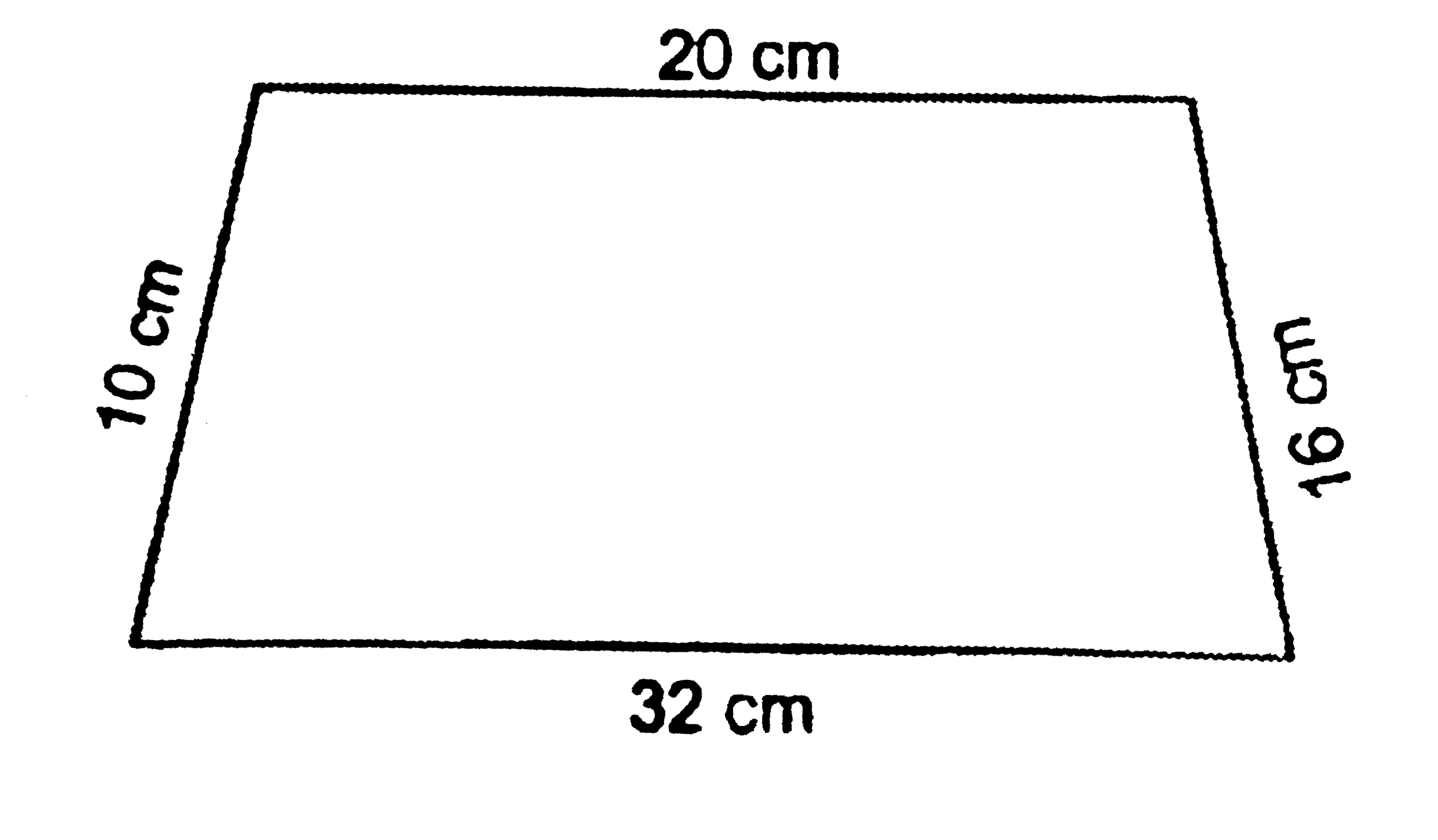
View SolutionFind the area of the trapezium given in given figure.
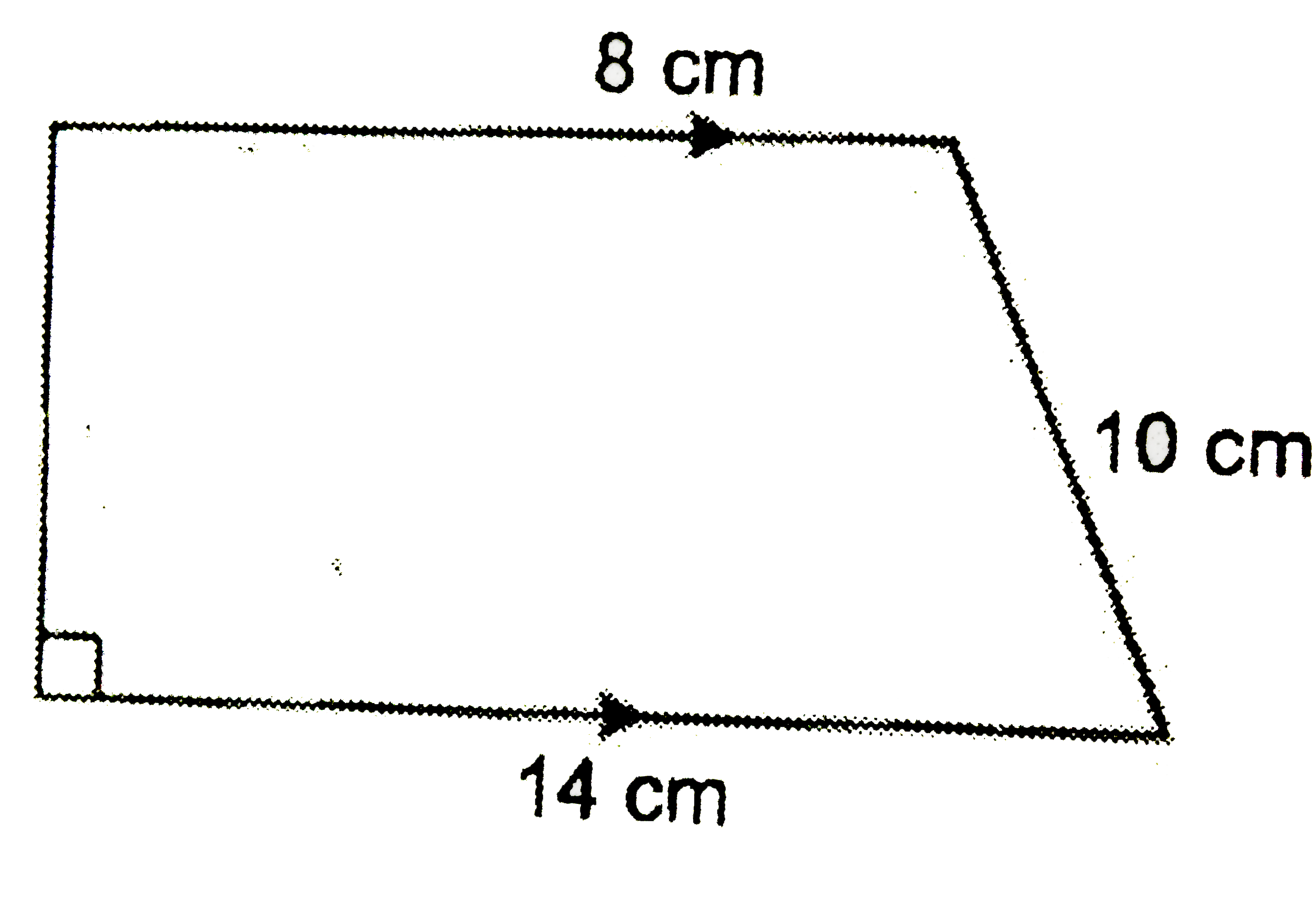
View SolutionThe three sides of a trapezium are equal each being 6 cms long. Let Δcm2 be the maximum area of the trapezium. The value of √3Δ is :
View SolutionFind the area of the trapezium given in adjoining figure.

View SolutionFind the area of trapezium in the given figure.
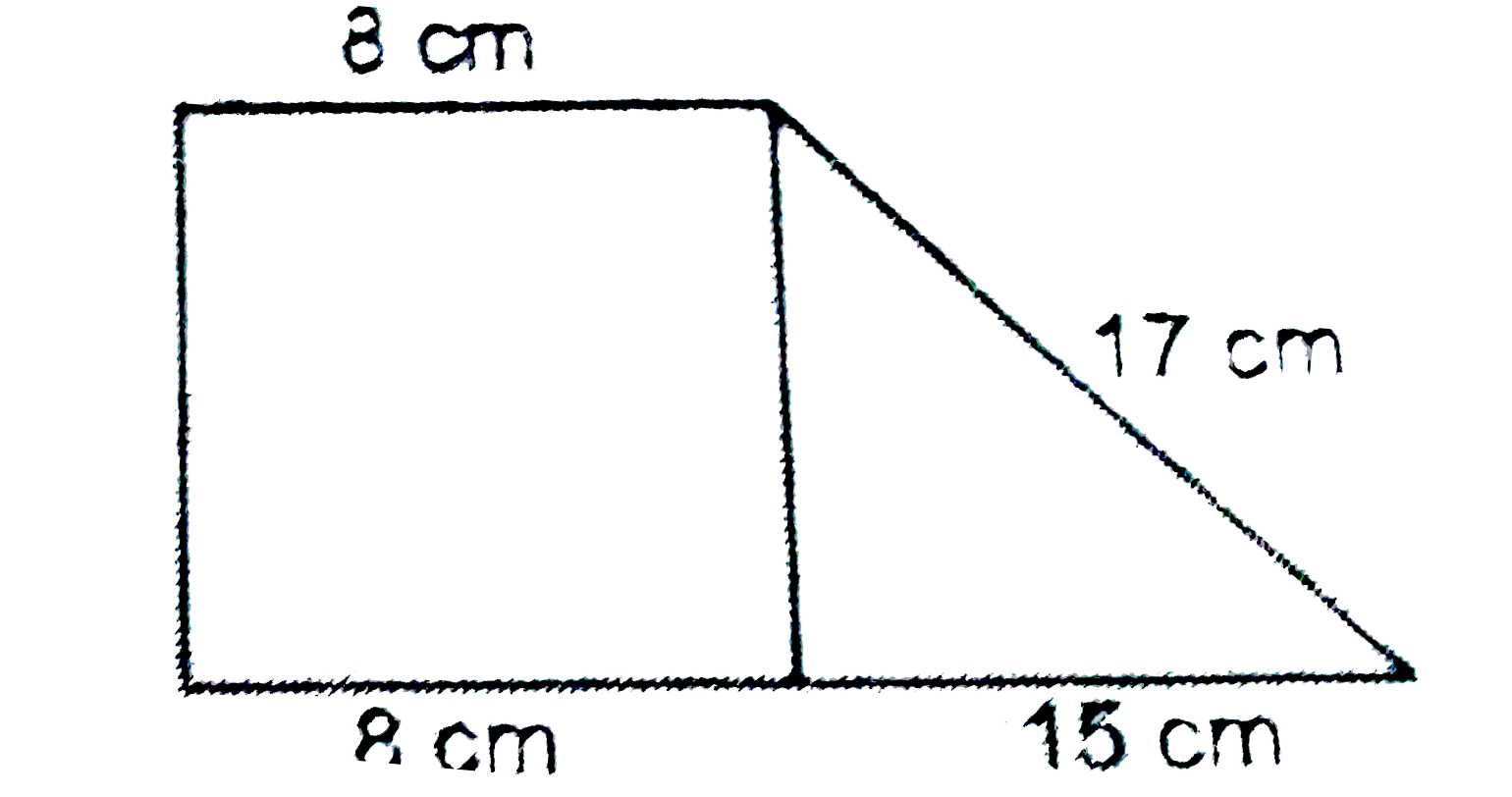
View SolutionThe parallel sides of a trapezium are 25cm and 13cm; its nonparallel sides are equal, each being 10cm, find the area of the trapezium.
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
View SolutionDraw the graphs of the following equations on the same graph paper: 2x+y=2; 2x+y=6 . Find the coordinates of the vertices of the trapezium formed by these lines. Also, find the area of the trapezium so formed.
View Solution
