The total number of solution of sin{x}=cos{x} (where {} denotes the fractional part) in [0,2π] is equal to 5 (b) 6 (c) 8 (d) none of theseSolution in Bengali
Given the equation is sin{x}=cos{x}.
tan{x}=1
tan(π/4)=1<tan1
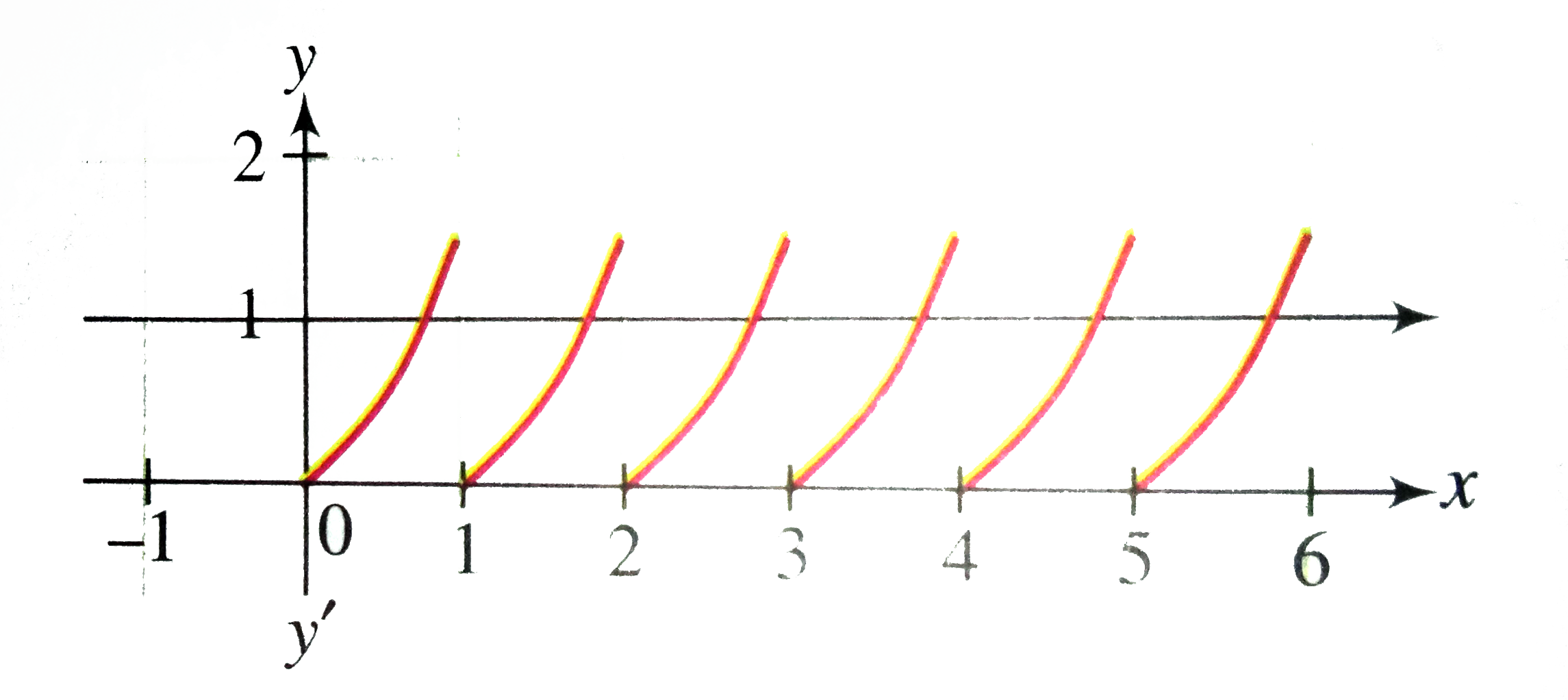
The graphs of y=tan{x} and y = 1 meet exactly six times in [0,2π].
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of y=1(1/x).
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionThe total number of solution of sin{x}=cos{x} (where {} denotes the fractional part) in [0,2π] is equal to 5 (b) 6 (c) 8 (d) none of these
View SolutionTotal number of solutions of [xpx2fx), where t] and denotes the greatest integer function and fractional part respectively is equal to (a) 2 (b) 4 (c) 6 (d) None of these
View SolutionThe total number of solutions of [x]2=x+2{x}, where [.] and {.} denote the greatest integer and the fractional part functions, respectively, is equal to: 2 (b) 4 (c) 6 (d) none of these
View SolutionThe number of solutions of
[sinx+cosx]=3+[−sinx]+[−cosx] in the internal [0,2π] is (where[.] denotes the the greatest integer function).
View SolutionThe total number of solution of cosx=√1−sin2x in [0,2π] is equal to (a) 2 (b) 3 (c) 5 (d) none of these
View SolutionThe total number of solution of sin{x}=cos{x} (where {} denotes the fractional part) in [0,2π] is equal to 5 (b) 6 (c) 8 (d) none of these
View SolutionThe total number of solutions of [x]2=x+2{x}, where [.] and {.} denote the greatest integer and the fractional part functions, respectively, is equal to: 2 (b) 4 (c) 6 (d) none of these
View SolutionThe total number of solution of sin{x}=cos{x} (where {} denotes the fractional part) in [0,2π] is equal to 5 (b) 6 (c) 8 (d) none of these
View SolutionThe total number of solutions of sin[x]=cos{x} (where {.} denotes the fractional part) in [0,2π] is equal
View SolutionThe total number of solutions of sin[x]=cos[x] where [⋅] denotes the fractional part ) in [0,2π] equal to
View SolutionThe number of solutions of
[sinx+cosx]=3+[−sinx]+[−cosx] in the internal [0,2π] is (where[.] denotes the the greatest integer function).
View SolutionThe total number of solution of cosx=√1−sin2x in [0,2π] is equal to 2 (b) 3 (c) 5 (d) none of these
View SolutionThe total number of solution of sin{x}=cos{x} (where {} denotes the fractional part) in [0,2π] is equal to 5 (b) 6 (c) 8 (d) none of these
View Solution
