The value of a for which the equation (1−a2)x2+2ax−1=0 has roots belonging to (0,1) isSolution in Punjabi
(a) a>0
(b) a<0
(c) a>2
(d) none of these
The correct Answer is:C
∵(1−a2)x2+2ax−1=0
1−a2≠0
x2−(2a1−a2)x−(11−a2)0
Let f(x)=x2+(2a1−a2)x−(1(1−a2))
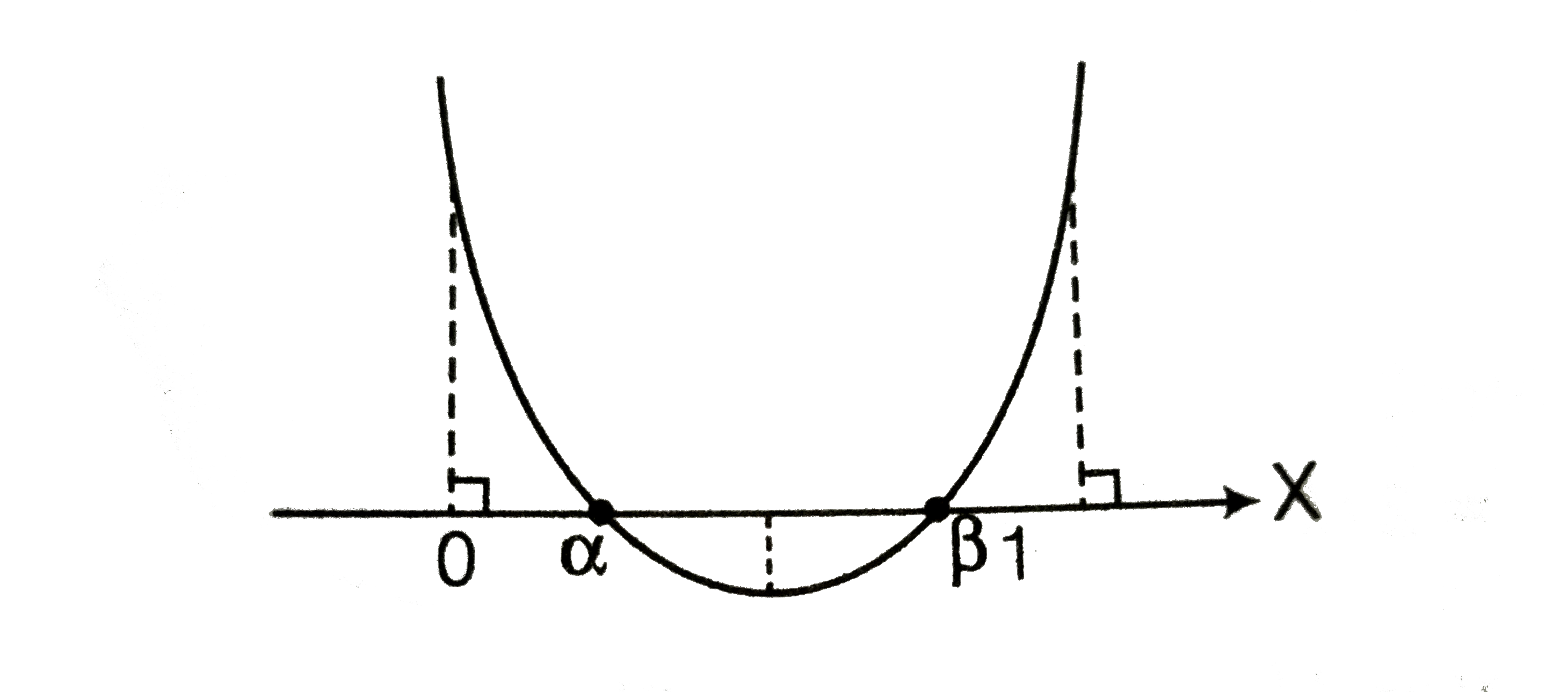
The following cases arise:
Case I D≥0 ltbr> (2a1−a2)2−4.1.(−11−a2)≥0
⇒4a2(1−a2)2+4(1−a2)≥0
⇒4a2+4−4a2(1−a2)2≥0
⇒4(1−a2)2≥0 [always true]
CaseII f(0)>0
⇒−1(1−a2)>0⇒11−a2<0
⇒1−a2<0
∴aε(−∞,o−1)∪(1,∞)
Case III f(1)>0
⇒1+2a(1−a2)−1(1−a2)>0
⇒1−a2+2a−1(1−a2)>0⇒a2−2a1−a2lg0

⇒a(a−2)(a+1)(a−1)>0
∴aε(−∞,−10∪(0,1)∪(2,∞)
Case Iv 0<x coordiane of vertex <1
⇒0<−2a2(1−a2)<1⇒0<aa2−1<1
⇒0<a(a+1)(a−1) an 1=aa2−1>0
⇒a(a+1)(a−1)>0

⇒aε(−1,0)∪(1,∞)
and (a−1+√52)(a−1−√52)(a+1)(a−1)>0
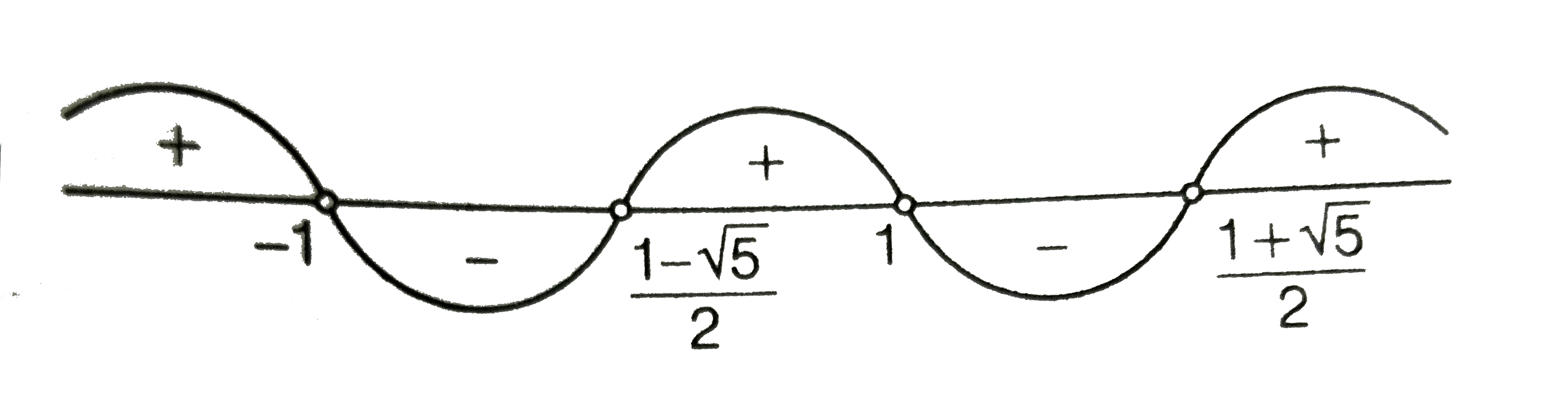
and aε(−∞,−1)∪(1−√52,1)∪(1+√52,∞)
∴aε(1−√52,0)∪(1+√52,∞)
Combining all cases, we get
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - SCQ_TYPE
1 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 5
10 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)
1 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
Similar Questions
From the graph of a quadratic polynomial y=ax2+bx+c,a,b,εR , Find its vertex, roots and D.
View SolutionIf 0<a<b<c and the roots α,β of the equation ax2+bx+c=0 are non-real complex numbers, then
View SolutionThe equation √x+1−√x−1=√4x−1 has
View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥0
View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
View SolutionIf t-1 and -t-1,t in R are the roots of (a+2)x^(2)+2ax-1=0, then complete set of values of 'a' is
View SolutionThe values of 'K' for which the equation |x|^(2)(|x|^(2)2k+1)=1-k^(2), has No root when k belongs to
View SolutionIf the roots of the equation 2ax3+(3b−9)x+1=0 are −2 and 3, then the value of a and b respec-tively are
View SolutionFor what values of the parameter a the equation x4+2ax3+x2+2ax+1=0 has atleast two distinct negative roots?
View SolutionNumber of integral values of 'a' for which (a-5)x^2 - 2ax + (a-4)=0 , has exactly one root in(0, 2), is
View SolutionThe equation x4+2ax3+x3+2ax+1=0 has at least two distinct negative roots is
View SolutionThe values of a for which both the roots of the equation (1−a2)x2+2ax−1=0 lie between 0 and 1 are given by
View SolutionIf the equation x2+2ax+b(a−1)=0 has real roots for all real value of a and b is an integer, then
View SolutionThe value of a for which both the roots of the equation (1−a2)x2+2ax−1=0 lie between 0 and 1, will always be greater than
View SolutionIf the equation x2−2ax+a2+a−3=0 has exactly one real root in (1,3) then largest integral value of a is
View SolutionThe equation x2+2(γ+1)x+a(a−4)=0 has negative roots only if γ belongs to the interval _________ .
View Solution
