The vertices of a triangle lie on the lines , respectively, and the side passes through the point . If is a rhombus lying in the first quadrant, being the origin, find the equation of the line
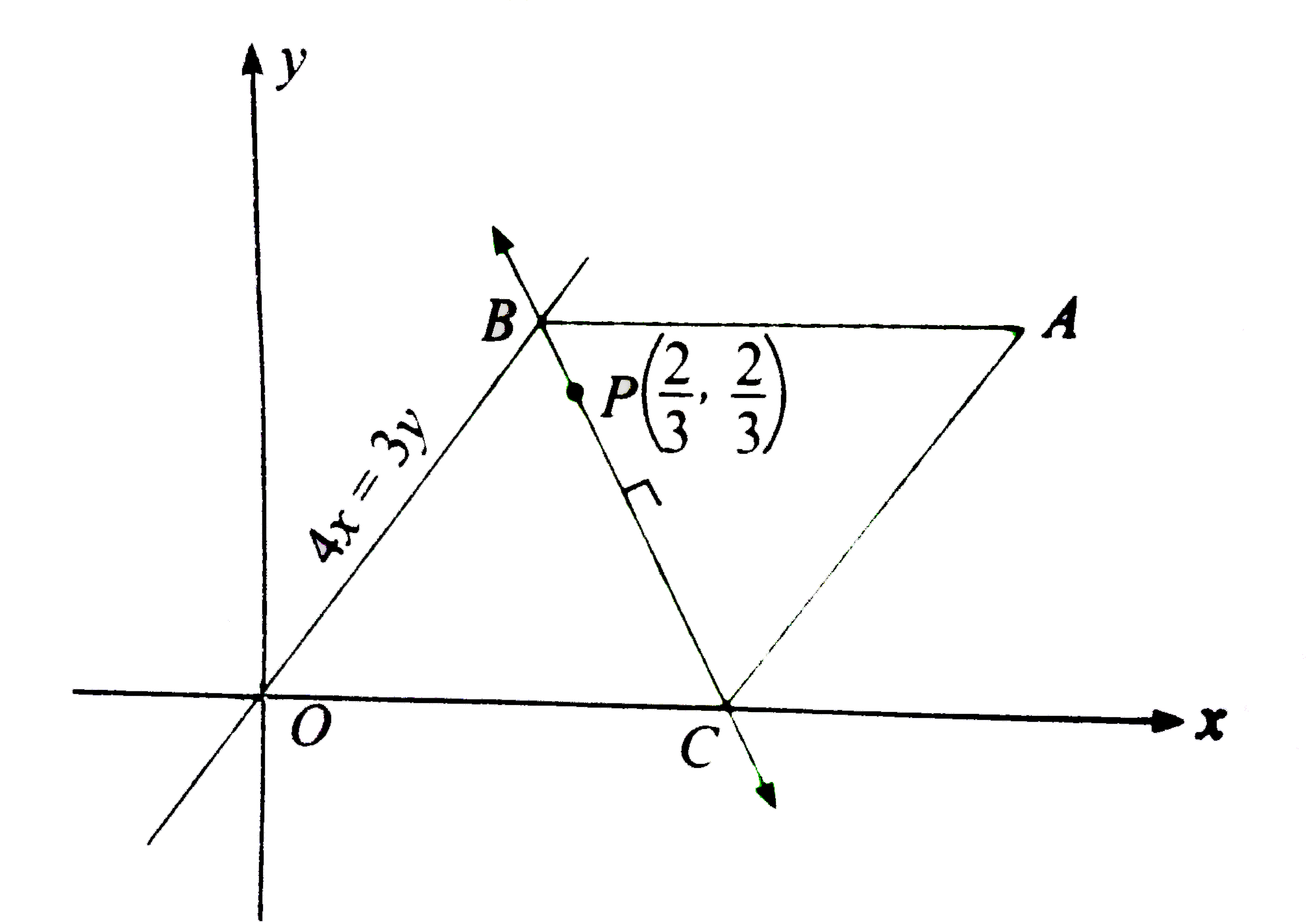
Diagonals of rhombus are equally inclined to the sides.
So, diagonals are parallel to or coincident with the angle bisectors of sides.
Equations of bisectors of sides OC and OB of rhombus are
or x-2y=0 and 2x+y=0
Clearly, diagonal BC is parallel to the bisector 2x+y=0.
So, equation BC is
or 2x+y-2=0
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.123videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.24videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
The vertices BandC of a triangle ABC lie on the lines 3y=4xandy=0 , respectively, and the side BC passes through the point (23,23) . If ABOC is a rhombus lying in the first quadrant, O being the origin, find the equation of the line BC.
View SolutionThe vertices B and C of a triangle ABC lie on the lines 3y=4x and y=0 respectively and the side BC passes through the point (23,23)If ABOC is a rhombus, O being the origin. If co-ordinates of vertex A is (α,β) , then find the value of 52(α+β).
View Solution
Knowledge Check
- Question 1 - Select One
If a+b+c=0 then the line 3ax+by+2c=0 passes through the fixed point
A(2,23)B(23,2)C(2,23)D(23,23)
The vertices B,C of a triangle ABC lie on the lines 4y=3xandy=0 respectively and the side BC passes through thepoint P(0,5). If ABOC is a rhombus, where O is the origin and the point P is inside the rhombus, then find the coordinates of A\'.
View SolutionFind the vector and Cartesian equations of the line passing through the points A(2,-3,0) and B(-2,4,3).
View SolutionThe line 2x+3y =6, 2x+3y=8 cut the X-axis at A, B respectively A line L= 0 drawn through the point (2,2) meets the axis at C in such a way that abscissa of A,B,C are in arithmetic Progression. then the equation of the line L is
View SolutionThe line 2x+3y=6,2x+3y−8 cut the X-axis at A,B respectively. A line L=0 drawn through the point (2,2) meets the X-axis at C in such a way that abscissa of A,B,C are in arithmetic Progression. then the equation of the line L is
View SolutionIf 3a+2b+4c=0 then the lines ax+by+c=0 pass through the fixed point
View SolutionA straight line through the point A(−2,−3) cuts the line x+3y=9 and x+y+1=0 at BandC respectively. Find the equation of the line if AB.AC=20.
View SolutionFind the vector equations of a line passing through the point A(3,-2,1) and parallel to the line joining B(-2,4,2) and C(2,3,,3). Also find the Cartesian equations of the line.
View Solution

